题目描述

Convert a Binary Search Tree to a sorted Circular Doubly-Linked List in place.

You can think of the left and right pointers as synonymous to the predecessor and successor pointers in a doubly-linked list. For a circular doubly linked list, the predecessor of the first element is the last element, and the successor of the last element is the first element.

We want to do the transformation in place. After the transformation, the left pointer of the tree node should point to its predecessor, and the right pointer should point to its successor. You should return the pointer to the smallest element of the linked list.

样例

Input: root = [4,2,5,1,3]

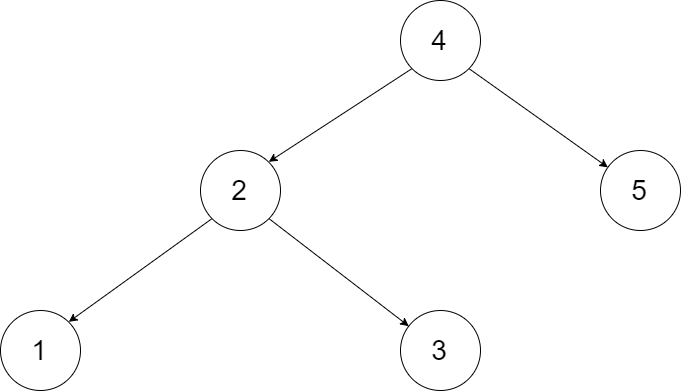
Output: [1,2,3,4,5]

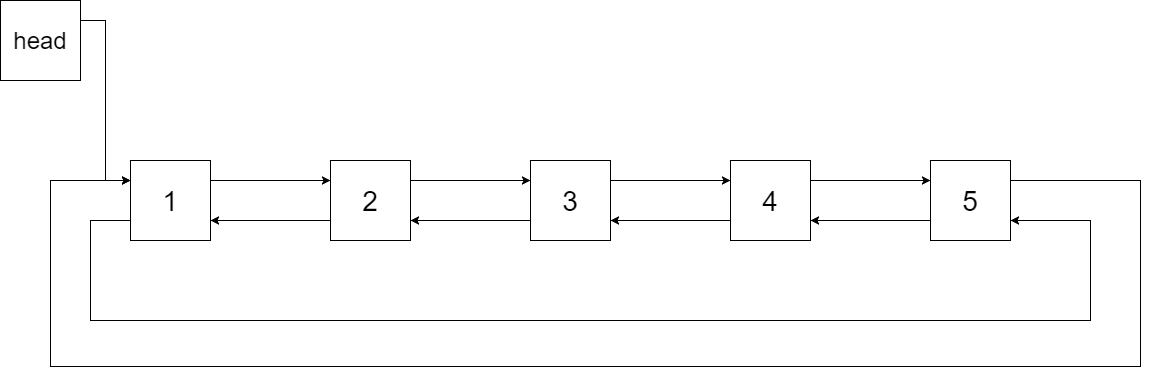
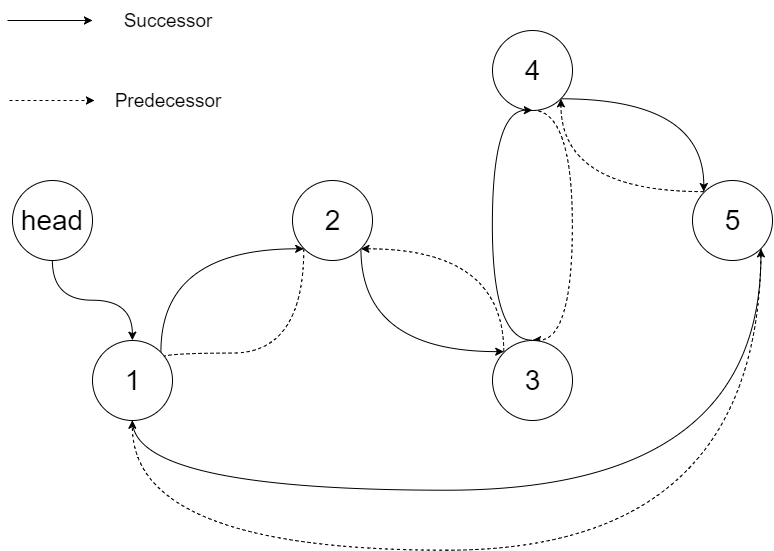
Explanation: The figure below shows the transformed BST. The solid line indicates the successor relationship, while the dashed line means the predecessor relationship.

算法1

(后序遍历) $O(n)$

假如BST是 (10 (6 1 8) (20 15 null))
转成链表是 1<->6<->8<->10<->15<->20，可知 10 的前驱是左子树的max，后继是右子树的min。
postorder traverse，拿到 left min & max, right min&max, 与root连接即可.

C++ 代码

    // return min node and max node in the tree
    pair<Node*, Node*> dfs(Node* root) {
        if(!root) return {nullptr, nullptr};

        auto left = dfs(root->left);
        auto right = dfs(root->right);

        // connect
        root->left = left.second;
        root->right = right.first;
        if(left.second) left.second->right = root;
        if(right.first) right.first->left = root;

        return { left.first? left.first : root, 
                right.second? right.second : root};
    }

    Node* treeToDoublyList(Node* root) {
        if(!root) return nullptr;

        auto p = dfs(root);
        // 将首尾相连
        p.first->left = p.second;
        p.second->right = p.first;
        return p.first;
    }