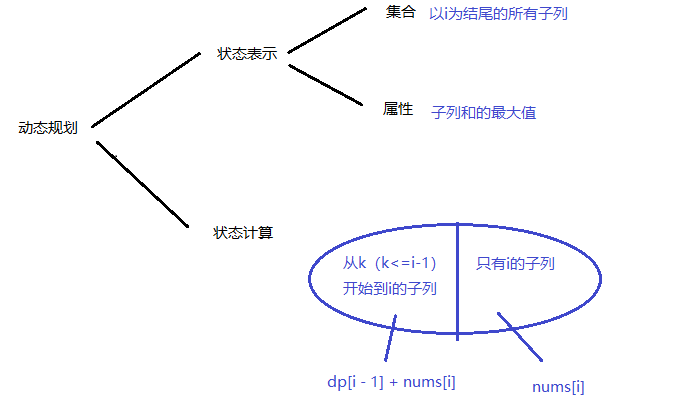
算法1

(动态规划) $O(n^2)$

时间复杂度

O(n)

参考文献

2019LeetCode暑期打卡活动

C++ 代码

class Solution {
public:
    int dp[100010];
    int maxSubArray(vector<int>& nums) {
        dp[0] = nums[0];
        for(int i = 1; i<nums.size(); i++){
            dp[i] = max(dp[i - 1], 0) + nums[i];
        }
        int res = INT_MIN;
        for(int i = 0; i<nums.size(); i++)
            res = max(res, dp[i]);
        return res;
    }
};

算法2

(动态规划-优化) $O(n^2)$

由于只用了一前面一个数，所以用变量存储之前的计算结果并且保存最大值即可。

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int last, res;
        last = 0, res= INT_MIN;
        for(int i = 0; i<nums.size(); i++){
            int now = max(last, 0) + nums[i];
            res = max(res, now);
            last = now;
        }
        return res;
    }
};