没有代码的数学题题解(超级简单,超级易懂)
Sulotion
我们可以发现一个点之所以不能被看见是因为点 $(x,y)$ 的 $gcd(x,y) > 1$,比如下面这张图:
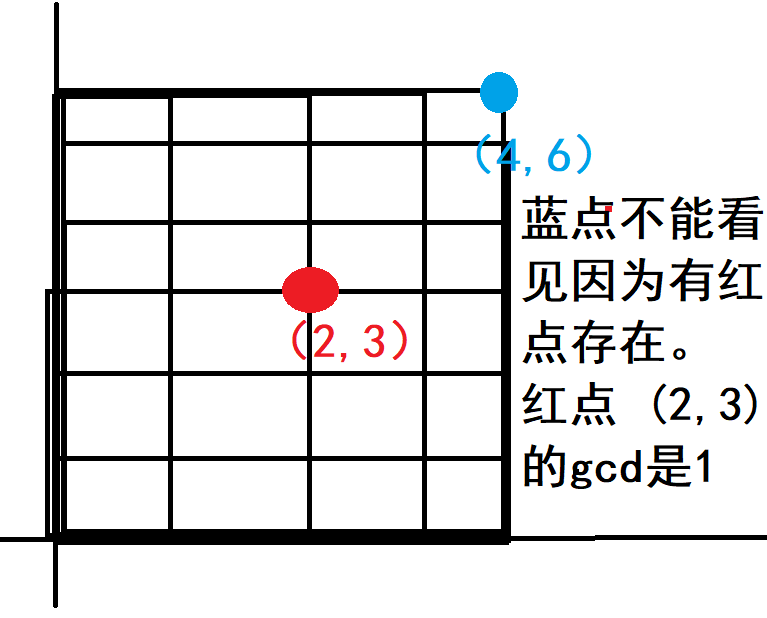
所以能看见的点 $(x,y)$ 一定有 $gcd(x,y)=1$
所以这个题目就是在求:
$$\sum_{i=1}^n \sum_{j=1}^n [gcd(i,j)=1]$$
当然结果还要 $+2$,因为有 $(1,0),(0,1)$ 这两个点。我们先考虑上式怎么求。
(Mobius反演大佬一看,“这不是sb题吗?”,我这个Mobius反演蒟蒻在一旁只能瑟瑟发抖)
不会莫反的同学不要紧,我们可以直接 欧拉函数 解决这个问题!!!
如果 $gcd(i,j)=1$,那么我们可以直接知道 $gcd(j,i)=1$,这个式子是对称的,那么我们可以令 $i>j$,只算一边,最后 $*2$。
但是这样会忽略 $(1,1)$ 这个点,我们得加上去。因此原式等于:
$$(2*\sum_{i=1}^n \sum_{j=1}^{i-1} [gcd(i,j)=1])+1$$
我们再来考虑 $\sum_{i=1}^n \sum_{j=1}^{i-1} [gcd(i,j)=1]$ 这部分这么算。经过观察发现 $\sum_{j=1}^{i-1} [gcd(i,j)=1]$ 这部分就是 $φ(i)$,因此等于:
$$\sum_{i=1}^n φ(i)$$
就是一个欧拉函数前缀和,用欧拉筛可以 $O(n)$ 解决,然而大佬们会杜教筛可以在非线性时间内解决。
把整个式子写完整,答案就是:
$$(2*\sum_{i=1}^n φ(i))+1+2$$
代码就不写了,没啥技术含量。。。
Summary
大佬们可以用莫反千千万万种方式切爆这题。

