看到$n <= 16 , k <= 5$ 的时候就应该想到状态压缩dp了
一开始先写了个暴搜, 发现可以改成记搜
设$a[i]$为每张卡牌的概率
先来画一下搜索树
设$f[depth][coins][state]$为当前要搜的状态, 从根节点开始做深搜（以n=3, k=1为例）的搜索树如下

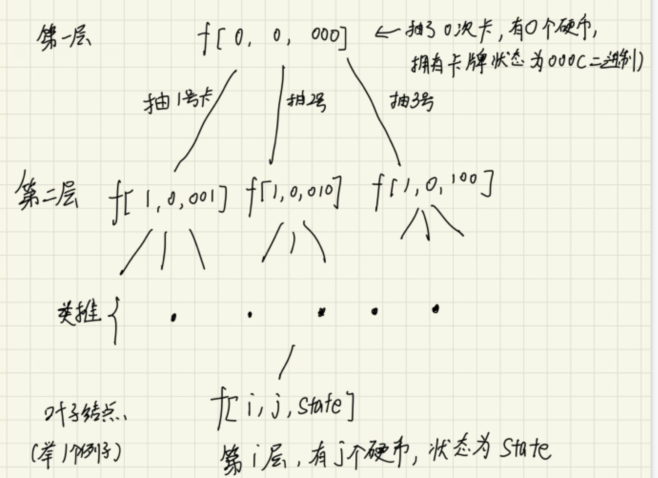
1.状态转移
先来讨论一下如何状态转移, 即$f[0][0][0]$如何从下一层的三个状态转移过来

1.我们发现下一层的三个状态在记搜的过程中都处理好了, 由于期望的定义, 应该有如下式子:
$f[0][0][0] = a[0] * f[1][0][001] + a[1] * f[1][0][010] + a[2] * f[1][0][100]$

2.递归终止边界处理
再来讨论一下叶子节点的$f[i][j][state]$要怎么判断是叶子节点和返回什么值

1.判断是否为叶子节点很简单, 将state里还没拥有的卡牌数量计数为cnt , 若$cnt * k <= j$, 即把没有的卡牌全部用硬币换需要的硬币数量小于等于已拥有的硬币数量, 就是叶子节点

2.返回什么值：我们发现期望的定义是概率乘以抽卡次数, 当前搜到最后一层的话, 由于搜到这一状态的概率已经在前面计算过了, 我们只需要返回抽卡次数(也就是i, 深度)即可

#include <bits/stdc++.h>
using namespace std;

int n, k;
double a[20];
double f[81][1 << 16];

double dp(int depth, int coin, int state, int cnt){
    if(f[coin][state]) return f[coin][state];      //标准的记搜板子
    if(cnt * k <= coin) return depth;       //判断是否是叶子节点
    double s = 0;
    for(int i = 0; i < n; i ++ ){    //枚举抽哪张卡
        if((state >> i) & 1)      //如果已经有这张卡了, 就让硬币数+1
            s += a[i] * dp(depth + 1, coin + 1, state, cnt);
        else
            s += a[i] * dp(depth + 1, coin, state | (1 << i), cnt - 1);   //如果没有这张卡, 就让状态更新
    }
    return f[coin][state] = s;
}

int main()
{
    cin >> n >> k;
    for(int i = 0; i < n; i ++ )
        cin >> a[i];

    cout << dp(0, 0, 0, n);

    return 0;
}