食物链

维护到祖宗结点距离的并查集

组成

$p$[ ]存储每个点的祖宗节点, $d[x]$存储$x$到$p[x]$的距离

int p[N], d[N];

操作

1. 初始化

初始化，假定节点编号是$1$ ~ $n$

每个结点的祖宗结点都是自己
每个结点到自己祖宗结点的距离都是$0$

for (int i = 1; i <= n; i ++ )
{
    p[i] = i;
    d[I] = 0;
}

2. 返回x的祖宗节点

与朴素版本相比，需要维护到祖宗结点的距离

这里有一个顺序问题，我们首先要记录$x$的祖宗结点，不能直接赋值
否则下面维护距离时候，$p[x]$不再是他的父节点，而是祖宗结点

int find(int x)
{
    if (p[x] != x)
    {
        int u = find(p[x]);
        d[x] += d[p[x]];
        p[x] = u;
    }
    return p[x];
}

3. 合并a和b所在的两个集合

需要额外维护距离信息

p[find(a)] = find(b);
d[find(a)] = distance; // 根据具体问题，初始化find(a)的偏移量

思路分析

本题将三类动物转化成对结点到祖宗结点距离来处理

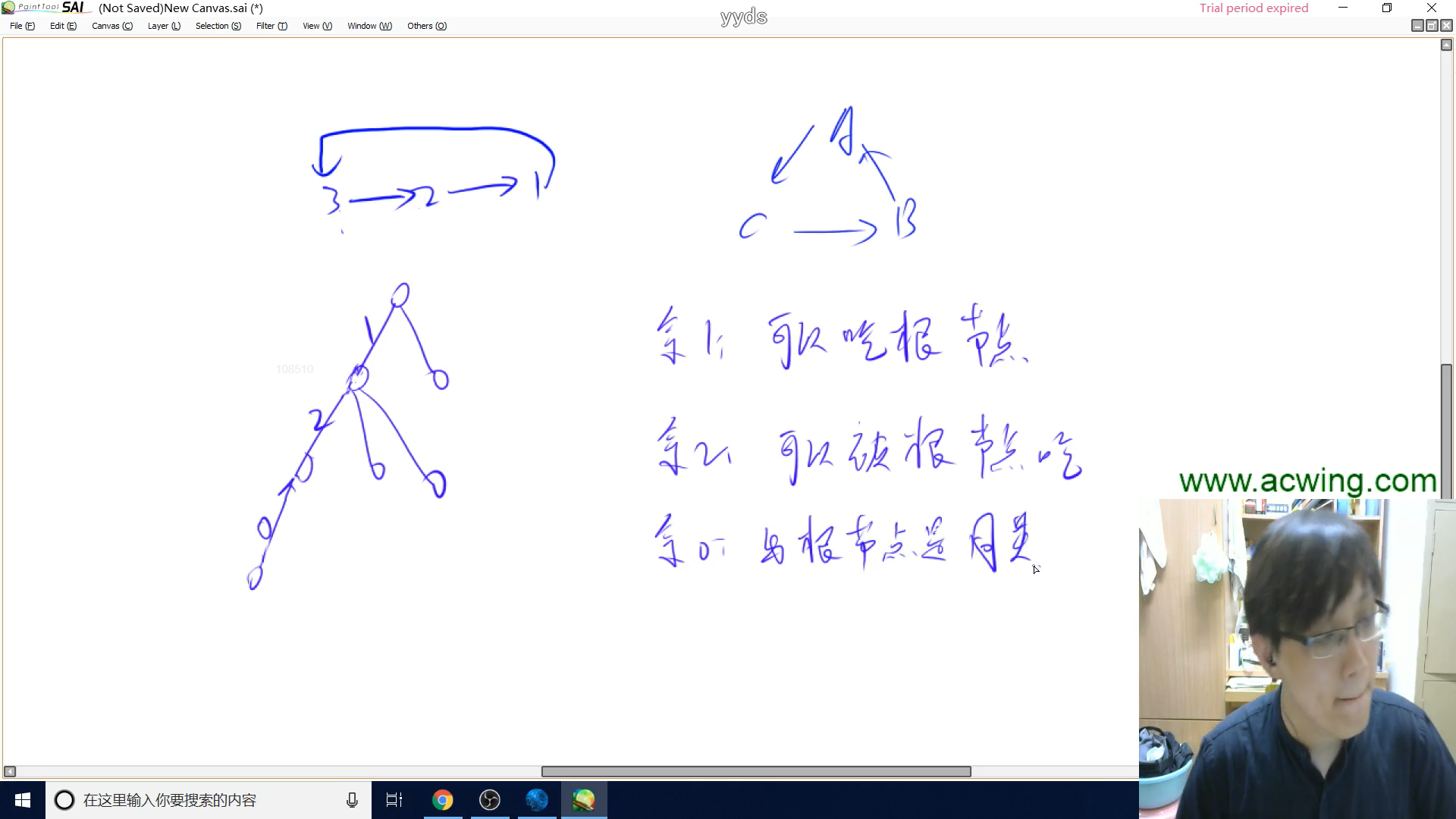
到根节点距离模3余1的表示的是可以吃根节点的动物
到根节点距离模3余2的表示的是可以吃距离为模3余1，并且被根节点吃的动物
到根节点距离为模3与0的表示与根结点是一类动物

是假话有两种可能
1. 范围越界
2. 与前面的话冲突

对于一句话，如果它越界了那么一定是假话

如果没有越界

是说法一

两个动物在一个集合里面，直接判断就行，两个结点到祖宗结点的距离模3同余即为真，反之为假

不在一个集合，默认是真的，那么就合并集合，二者距离在模三下相等，这里注意，我们的距离是允许是负值的，只要模三意义下相等就行，所以维护距离的时候。比如说模三余0，等式右边可以暴力写0

是说法二

在一个集合，就直接取模判断

不在一个集合，就默认是真的，合并集合即可

代码

#include <iostream>

using namespace std;

const int N = 50010;

int n, m;
int p[N], d[N];

int find(int x) // 路径压缩 + 查询祖宗结点
{
    if (p[x] != x)
    {
        int t = find(p[x]);
        d[x] += d[p[x]];
        p[x] = t;
    }
    return p[x];
}

int main()
{
    scanf("%d%d", &n, &m);

    for (int i = 1; i <= n; i ++ ) p[i] = i;

    int res = 0;
    while (m -- )
    {
        int t, x, y;
        scanf("%d%d%d", &t, &x, &y);

        if (x > n || y > n) res ++ ; // 越界
        else
        {
            int px = find(x), py = find(y); // 因为下面要频繁用到x与y的祖宗结点，这里先求出来，下面直接用
            if (t == 1) // 说法一
            {
                if (px == py && (d[x] - d[y]) % 3) res ++ ; //在一个集合，判断
                else if (px != py) // 不在一个集合，合并集合
                {
                    p[px] = py;
                    d[px] = d[y] - d[x];
                }
            }
            else  // 说法二
            {
                if (px == py && (d[x] - d[y] - 1) % 3) res ++ ; // 在一个集合，判断
                else if (px != py) // 不在一个集合合并集合
                {
                    p[px] = py;
                    d[px] = d[y] + 1 - d[x];  // 维护距离
                }
            }
        }
    }

    printf("%d\n", res);

    return 0;
}