最大异或对

这次y总打卡代码风格和课上风格差别有点大，所以采用课上的代码了，更容易看懂些

思路分析

暴力做法

对于每一个数进行枚举，时间复杂是$O(n ^ 2)$的，很明显会超时

虽然我们可以发现，前后具有重复性，可以缩小一半计算量，不过对于时间复杂度来说依然没有减小，常数变了下而已

$trie$树

首先，对于一个数字，和它异或最大的数是从最高位向最低位按位取反的数

我们每次选择都是尽量选择本位与它不相同的，这样我们才可以取到最大异或值

我们可以考虑把数字按照二进制存储进$trie$树，二进制数也是一种字符串嘛，存储时候每个字符串都是31位长，所以说不用标记以某个结点结尾的个数了，叶结点就表示走到了尽头

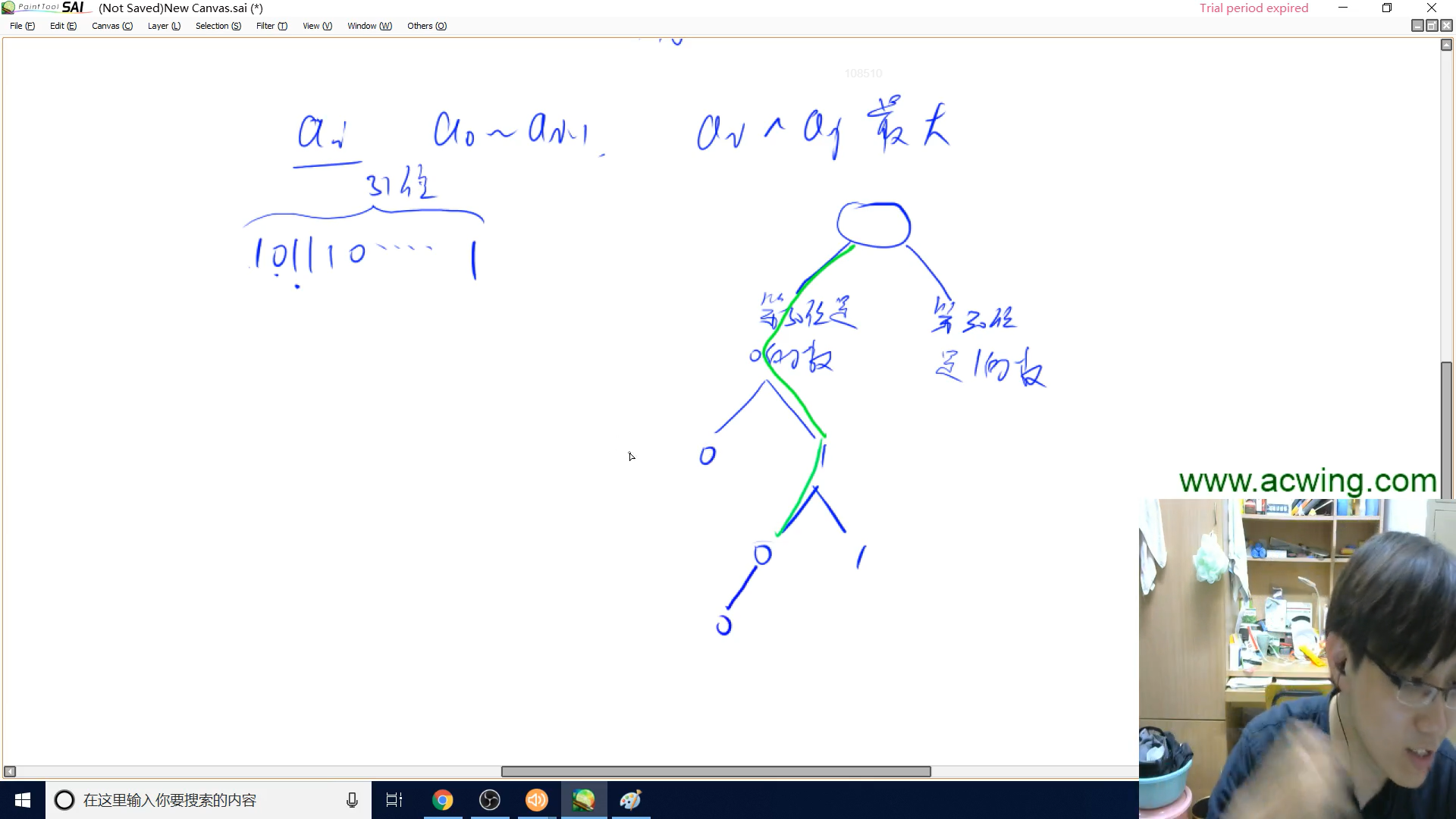
剩下的就是$trie$树的基本操作，没有新的知识点了

共有十万个数，每个数有31个结点，所以我们结点个数就是三百一十万

时间复杂度分析

$trie$树构造好后，我们可以用$O(n)$的时间复杂度得到答案

对于每个数字找到它的最大异或对是$31$次运算，而之前暴力做法则是十万次，效率明显提高

代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010, M = 31 * N;

int n;
int a[N];
int son[M][2], idx;

void insert(int x)
{
    int p = 0;
    for (int i = 30; i >= 0; i -- )
    {
        int u = x >> i & 1; // 取出数字的当前位
        if (!son[p][u]) son[p][u] = ++ idx;
        p = son[p][u];
    }
}

int query(int x) // query() 得到的是某一个数的最大异或对，不是异或值，最后还需要加一步运算
{
    int p = 0, res = 0;
    for (int i = 30; i >= 0; i -- )
    {
        int u = x >> i & 1;
        if (son[p][!u])
        {
            p = son[p][!u];
            res = res * 2 + !u; // 最大异或对是之前位数左移一位再加上当前位数
        }
        else
        {
            p = son[p][u];
            res = res * 2 + u;
        }
    }
    return res;
}

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);

    int res = 0;

    for (int i = 0; i < n; i ++ )
    {
        insert(a[i]); // 插入
        int t = query(a[i]);
        res = max(res, a[i] ^ t); // 求最大异或值
    }

    printf("%d\n", res);

    return 0;
}