算法提高课汇总

算法思路

理解题意

对于每个格子都有2种选择: 横着放(横块)或竖着放(竖块). 如果把每个格子的2种选择都枚举一遍那么
时间复杂度会来到指数级别.

核心思路: 只考虑横块的摆放, 最后判断剩余位置是否能恰好放入竖块. 若能则摆放方案合法, 否则不
合法.

最后方案数(乘法原理) $ = $ 横方案数$\times$竖方案数 = 横方案数$\times$1 $=$ 横着摆放的方案数.

$DP$分析

按列从左向右摆放横块, 考虑当前列不同状态对应的合法摆放方案数.

状态表示 $dp(i, j)$

• 集合: 从前$i - 1$列摆放横块, 且第$i$列的状态为$j$(二进制表示)的所有摆放方案.

• 属性: Count合法方案数

例如下图对应状态: $dp(i, \lbrace 10110\rbrace) = dp(i, 22)$

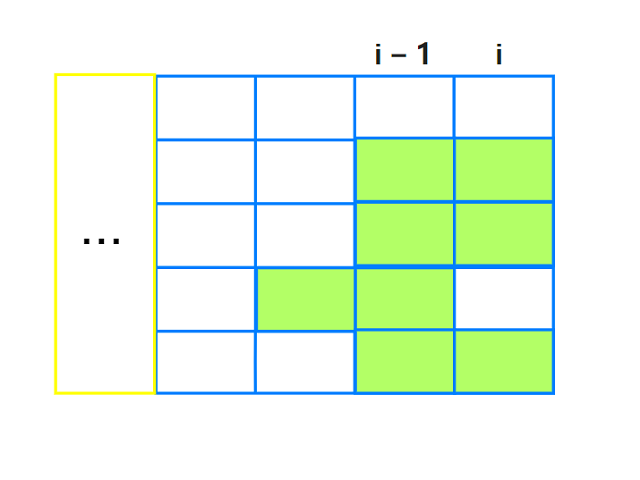
状态的定义保证计算的是前$i - 1$列合法方案的数目, 第$i$列状态为$j$—没有对其合法性做要求.

状态计算

对于$dp(i, j)$, 根据$j$我们确定了第$i - 1$列的摆放状态(只有$i - 1$列的横块会到第$i$列), 我们
以第$i - 2$列的摆放方案也就是$dp(i - 1, k)$作为上一个状态($k$确定第$i - 2$列摆放方案).

• $dp(i, j) = \sum_kdp(i - 1, k)$, 且对应$k$保证前$i - 1$列是合法状态.

如何确定$k$对于$j$是合法状态?

1. $k$与$j$不能在行上有交集(否则重叠). <--> $k\&j = 0$.

2. 第$i - 1$列的状态合法(列连续空格数目为偶数, 即可以放入竖块). <--> 第$i - 1$列由$k$和$j$
   共同确定, 即状态$k\mid j$合法.

代码实现

时间复杂度: 状态数目 $\times$ 状态计算 = $N2^M \times 2^M$. 可以通过预处理状态计算时每个$j$对应
的合法$k$以降低时间复杂度.

具体代码:

#include <vector>
#include <cstring>
#include <iostream>

using namespace std;

typedef long long ll;

const int N = 11, M = 12, S = 1 << N;

int n, m;
bool st[M]; //st[j] = true, 列状态j合法, 可以放入竖块
ll dp[M][S];
vector<int> state[S]; //state[j] = {k1, k2, ...}, 对于j的合法的k

int main()
{
    while( cin >> n >> m, n || m )
    {
        //st[]
        for( int i = 0; i < 1 << n; i ++ )
        {
            int cnt = 0; //连续空格数目
            bool is_valid = true; //是否合法
            for( int j = 0; j < n; j ++ )
            {
                if( i >> j & 1 )
                {//不是空格
                    if( cnt & 1 )
                    {//之前的空格数为奇数, 不合法
                        is_valid = false;
                        break;
                    }
                    else cnt = 0; //目前合法, 清零(也可以不做)
                }
                else    cnt ++ ; //空格数+1
            }
            if( cnt & 1 )   is_valid = false; //如果最后都是空格 需要最后判断一次
            st[i] = is_valid;
        }

        //state
        for( int j = 0; j < 1 << n; j ++ )
        {
            state[j].clear();
            for( int k = 0; k < 1 << n; k ++ )
            {
                if( (j & k) == 0 && st[j | k] ) state[j].push_back(k);
            }
        }

        //dp
        memset(dp, 0, sizeof dp);
        dp[0][0] = 1; //第一列(下标从0开始) 前-1列无法摆放横块, 所以方案数为1---不放
        for( int i = 1; i <= m; i ++ )
            for( int j = 0; j < 1 << n; j ++ )
                for( auto k : state[j] )
                    dp[i][j] += dp[i - 1][k];
        cout << dp[m][0] << endl; //前0~m-1列合法, 且第m列状态为0(前m-1列恰好摆满)
    }
    return 0;
}