算法提高课汇总

算法思路

理解题意

1. 限制

   • 构建长度为$n$的字符串$S$不包含给定字串$T$.

2. 目的

   • 满足限制的字符串个数.

3. 核心思路: 一个字符串不包含子串$T$<-->在使用KMP算法用$T$匹配$S$的过程中, $j\not= m$.($m$为子串$T$的长度).

4. 应用状态机模型: 将KMP算法中$j$的所有可能值($0\sim m$)作为状态, 状态间的转移由$S$对应字符及
   kmp算法的计算过程确定.

状态机模型

• 状态: KMP算法匹配过程中模式串的下标值$j$.

• 有向边: 随着文本串$S$的下标$i = i + 1$, $j$由KMP算法所转移的下标值.

• 入口: 初始$j$的值为0.

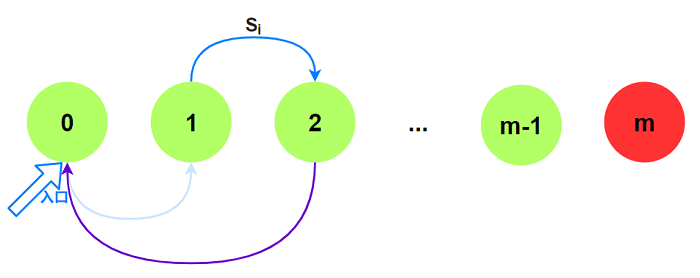
一条长度为$n$且不经过状态$m$的路径与一个长度为$n$且不含子串$T$的字符串一一对应.

$DP$分析

状态定义$dp(i, j)$

• 集合: 从入口出发路径长度为$i$, 最终落在状态$j$的所有路径; 当前构建的字符长度为$i$, 且对应
  KMP计算下标为$j$的所有字符串.

• 属性: Count

状态计算

状态机模型, 不过本题不同于之前计算方式—当前状态从何而来; 而是用当前状态能到哪个状态, 也就是
顺着转移的方向用当前状态更新其后续状态, 契合kmp的计算过程.

$f(i + 1, k) =\sum_{j}f(i, j)$, $k$是$j$经过KMP计算后的下标值.

最后题解即为长度为$n$且最终状态不为$m$的路径数目.

代码实现

#include <cstring>
#include <iostream>

using namespace std;

const int N = 55, mod = 1e9 + 7;

int n;
char t[N];
int nxt[N], dp[N][N];

int main()
{
    cin >> n >> (t + 1);

    int m = strlen(t + 1);
    //nxt[]
    for( int i = 2, j = 0; i <= m; i ++ )
    {
        while( j && t[j + 1] != t[i] ) j = nxt[j];
        if( t[j + 1] == t[i] )  j ++ ;
        nxt[i] = j;
    }

    //dp
    dp[0][0] = 1; //入口
    for( int i = 0; i < n; i ++ )
    {
        for( int j = 0; j < m; j ++ )
        {
            for( char c = 'a'; c <= 'z'; c ++ )
            {//c是构建的字符S[i]
                int k = j;
                while( k && t[k + 1] != c ) k = nxt[k];
                if( t[k + 1] == c ) k ++ ;
                dp[i + 1][k] = ( dp[i + 1][k] + dp[i][j] ) % mod;
            }
        }
    }

    int res = 0;
    for( int i = 0; i < m; i ++ )   res = ( res + dp[n][i] ) % mod;
    cout << res << endl;

    return 0;
}