算法1

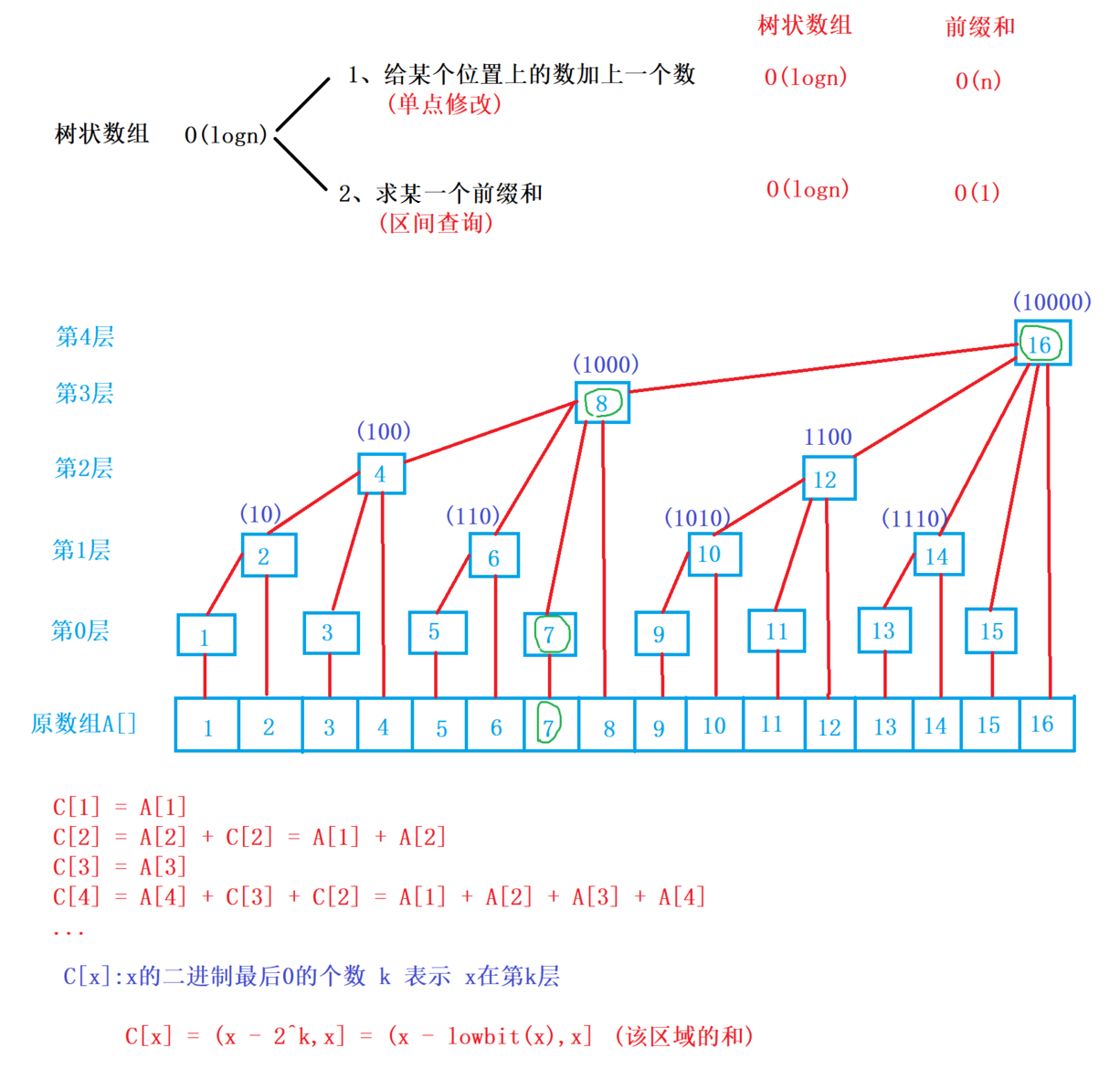
树状数组

• 1、lowbit(x):返回x的最后一位1

• 2、add(x,v):在x位置加上v，并将后面相关联的位置也加上v

• 3、query(x):询问x的前缀和

时间复杂度 $O(logn)$

参考文献

蓝桥杯辅导课

Java 代码

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
    static int N = 100010;
    static int n;
    static int m;
    static int[] a = new int[N];
    static int[] tr = new int[N];

    public static int lowbit(int x)
    {
        return x & -x;
    }
    //在x位置加上v，并将后面相关联的位置也加上v
    public static void add(int x,int v)
    {
        for(int i = x;i <= n;i += lowbit(i)) tr[i] += v;
    }
    //前缀和
    public static int query(int x)
    {
        int res = 0;
        for(int i = x;i >= 1;i -= lowbit(i)) res += tr[i];
        return res;
    }
    public static void main(String[] args) throws IOException {
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        String[] s1 = reader.readLine().split(" ");
        n = Integer.parseInt(s1[0]);
        m = Integer.parseInt(s1[1]);
        String[] s2 = reader.readLine().split(" ");
        for(int i = 1;i <= n;i++) a[i] = Integer.parseInt(s2[i - 1]);
        //搭建树状数组
        for(int i = 1;i <= n;i++) add(i,a[i]);

        while(m -- > 0)
        {
            String[] s3 = reader.readLine().split(" ");
            int k = Integer.parseInt(s3[0]);
            int x = Integer.parseInt(s3[1]);
            int y = Integer.parseInt(s3[2]);
            //k = 0 是询问[x,y]的区间和，k = 1是在x位置添加y元素
            if(k == 0) System.out.println(query(y) - query(x - 1));
            else add(x,y);
        }
    }
}

算法2

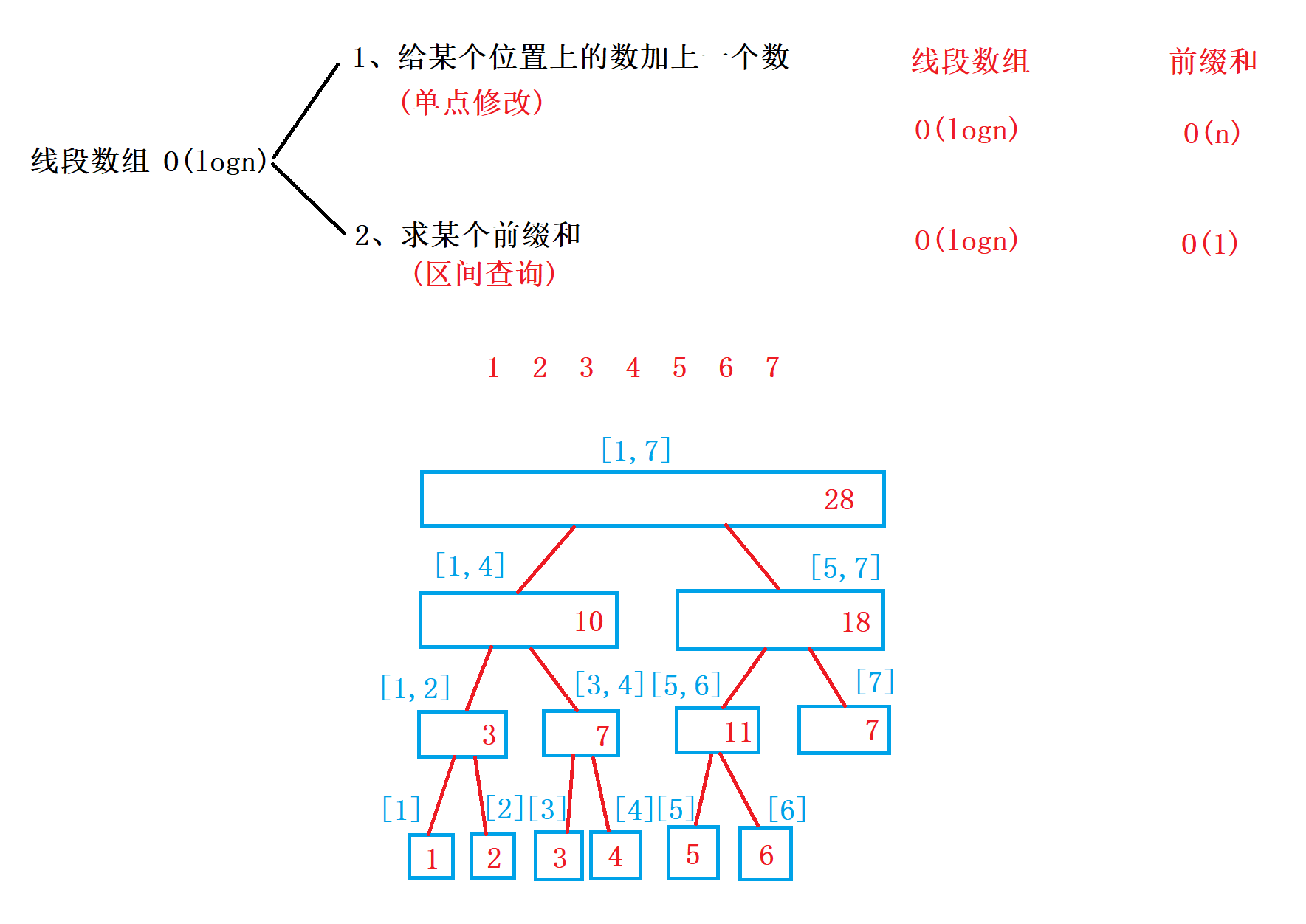
线段树

• 1、pushup(u):用子节点信息来更新当前节点信息（把信息往上传递）

• 2、build(u,l,r):在一段区间上初始化线段树，其中u表示根结点，l表示左边界，r表示右边界

• 3、query(u,l,r):查询某段区间的和，其中u表示根结点，l表示左边界，r表示右边界

• 4、modify(u,x,v):修改操作，在u结点中，x位置加上v

修改操作

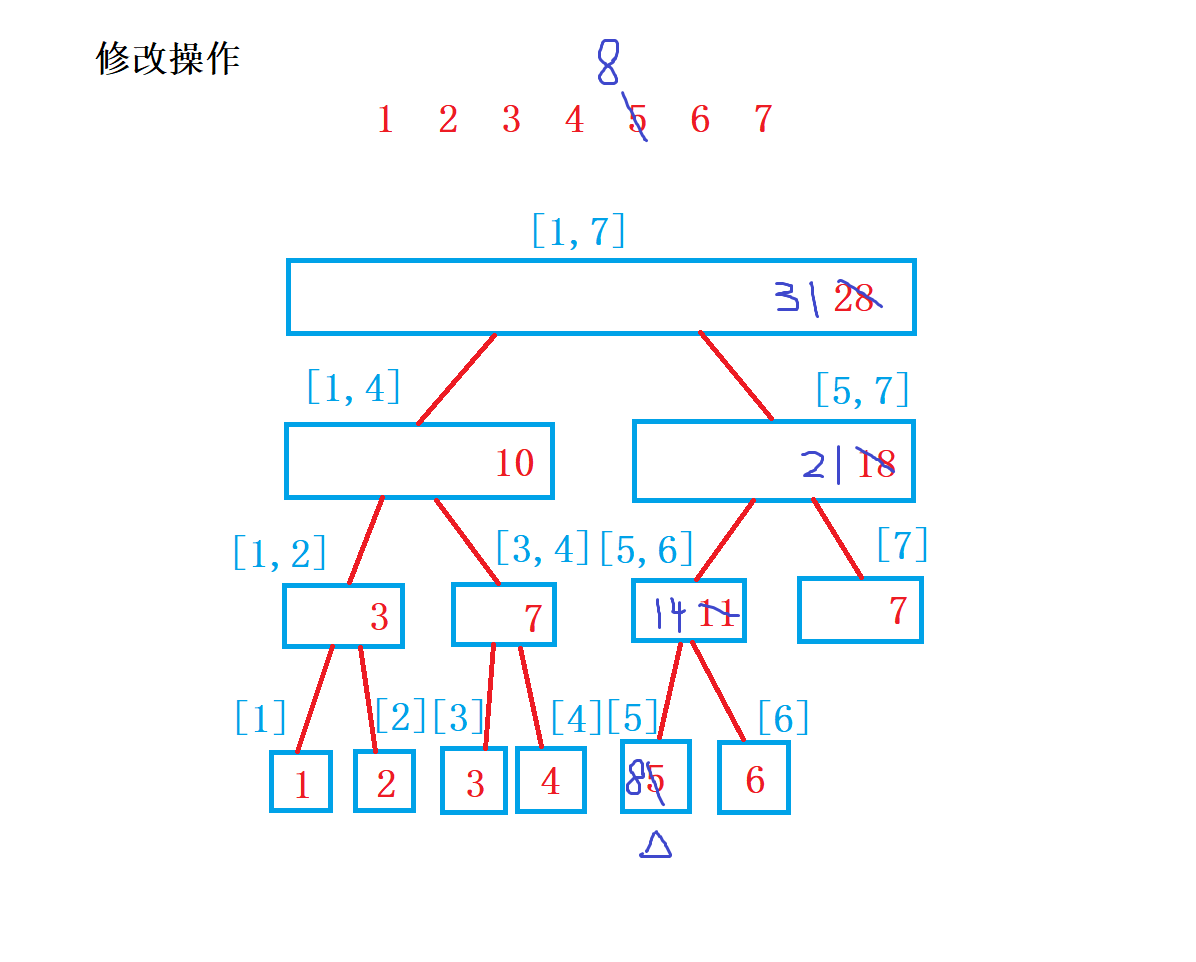
查询操作

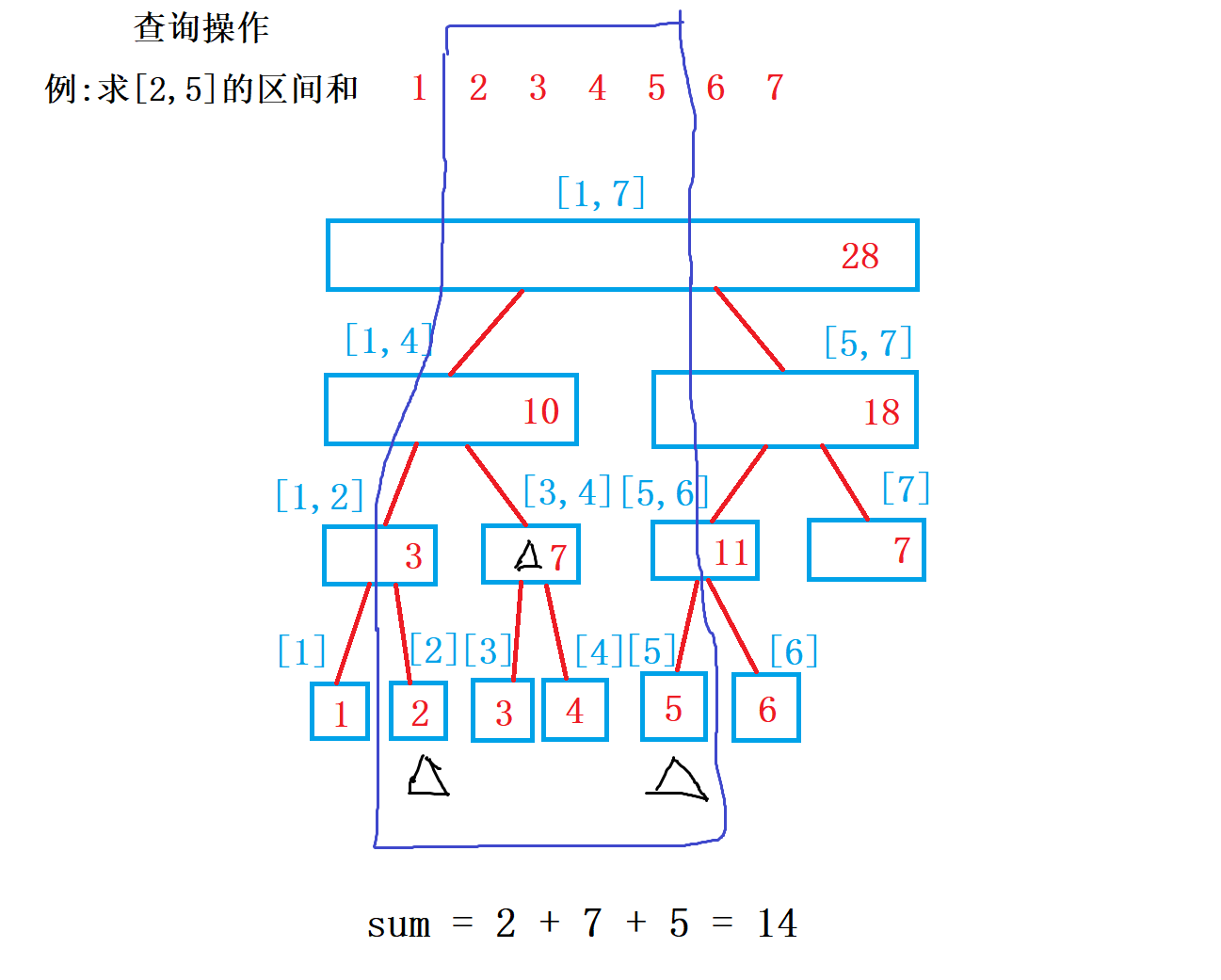
时间复杂度 $O(logn)$

参考文献

蓝桥杯辅导课

Java 代码

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
    static int N = 100010;
    static int n;
    static int m;
    static int[] w = new int[N];
    static Node[] tr = new Node[N * 4];
    //用子节点信息来更新当前节点信息（把信息往上传递）
    public static void pushUp(int u)
    {
        tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
    }
    //在一段区间上初始化线段树，其中u表示根结点，l表示左边界，r表示右边界
    public static void build(int u,int l,int r)
    {
        if(l == r) tr[u] = new Node(l,r,w[r]);
        else
        {
            tr[u] = new Node(l,r,0);
            int mid = l + r >> 1;
            build(u << 1,l,mid);
            build(u << 1 | 1,mid + 1,r);
            pushUp(u);
        }
    }
    //查询某段区间的和，其中u表示根结点，l表示左边界，r表示右边界
    public static int query(int u,int l,int r)
    {
        if(tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
        int mid = tr[u].l + tr[u].r >> 1;
        int sum = 0;
        if(l <= mid) sum = query(u << 1,l,r);
        if(r > mid) sum += query(u << 1 | 1,l,r);
        return sum;
    }
    //修改操作，在u结点中，x位置加上v
    public static void modify(int u,int x,int v)
    {
        if(tr[u].l == tr[u].r) tr[u].sum += v;
        else
        {
            int mid = tr[u].l + tr[u].r >> 1;
            if(x <= mid) modify(u << 1,x,v);
            else modify(u << 1 | 1,x,v);
            pushUp(u);
        }
    }
    public static void main(String[] args) throws IOException {
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        String[] s1 = reader.readLine().split(" ");
        n = Integer.parseInt(s1[0]);
        m = Integer.parseInt(s1[1]);
        String[] s2 = reader.readLine().split(" ");
        for(int i = 1;i <= n;i++) w[i] = Integer.parseInt(s2[i - 1]);
        //搭建线段树
        build(1,1,n);

        while(m -- > 0)
        {
            String[] s3 = reader.readLine().split(" ");
            int k = Integer.parseInt(s3[0]);
            int x = Integer.parseInt(s3[1]);
            int y = Integer.parseInt(s3[2]);
            //k = 0 是询问[x,y]的区间和，k = 1是在x位置添加y元素
            if(k == 0) System.out.println(query(1,x,y));
            else modify(1,x,y);
        }
    }
}
//段结点
class Node
{
    public int l;//左边界
    public int r;//右边界
    public int sum;//当前块的总和

    public Node(int l,int r,int sum)
    {
        this.l = l;
        this.r = r;
        this.sum = sum;
    }
}