算法提高课汇总

写在前面

• KMP利用匹配串的额外信息, 使得其优于朴素方法 – 当前位置不匹配, 直接
  跳到下一格继续匹配. KMP向后跳的步数是下一个可能的位置, 而不是简单的每次
  向后一格.

• 为何使用最长的前后串匹配, 并不是要向后跳得更快以使算法运行更快, 而是那是
  下一个可能的位置, 如果不是最长, 我们可能会错过一个可能的匹配.

• KMP判断匹配位置时的状态: 当前两个字符串匹配的最长串, 所以该逻辑也可以
  预处理构造匹配串的前后缀匹配信息.

算法思路

KMP算法由 $Knuth−Morris−Pratt$ 三位科学家提出，可用于在一个文本串中寻找某模式串
存在的位置. 本算法可以有效降低在一个文本串中寻找某模式串过程的时间复杂度.

设$S$为文本串; $P$为模式串. 为理解KMP, 首先考虑暴力算法.

暴力比较 $O(n^2)$

暴力算法思路: 某时刻以$S_i$为起点判断$S_{i\sim m}$中是否存在模式串$P$. 暴力思路: 向后依次与$P_j$判断
是否相等: 若相等, 两个指针后移继续判断, 直到到达$P$的最后一个字母; 如果不相等则指针$i$后移
一位, 重新与整个$P$从$1$开始判断.

假设2个字符串从$S$的某处开始匹配:

按暴力算法思路, 它们会一直判断字符相等直到:

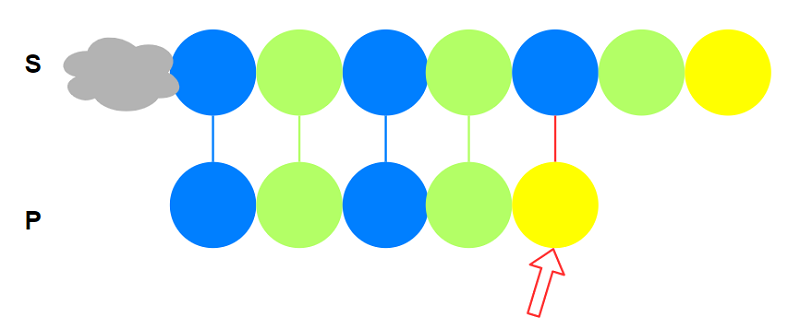
不相等, 则$i$后移一位, 重新与$P$匹配:

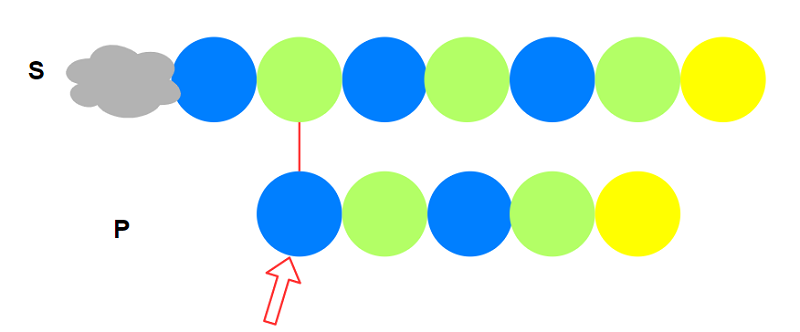
不相等, 则$i$后移一位, 重新与$P$匹配:

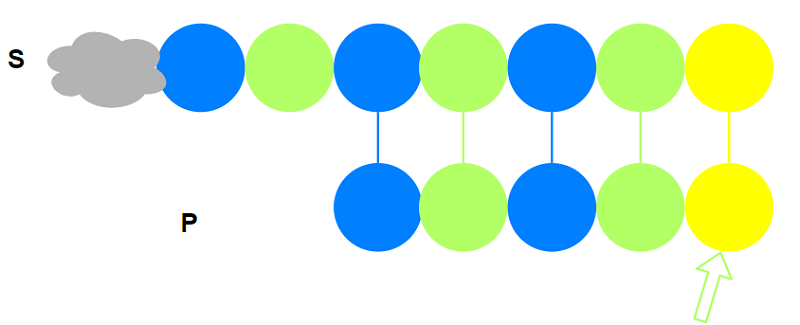
匹配到$P$的最后一个字符: 匹配成功. $i$后移一位(如果还有)继续与$P$从头开始匹配$…$

小结

暴力算法每次在匹配失败时用到了一个信息: 在这个位置匹配失败!(好像是废话). 接着就寄希望于
当前起点的下一位, 希望从它开始可以与$P$匹配.

暴力思路的优化

设想如果我们提前了解到$P$的某些方面的信息, 能否稍微优化这种思路呢.

1. $P$所有单词个不相同

这个时候好像我们只好使用暴力的思路了, 只能不断尝试下一个$S$是否能作为匹配起点.

2. $P$有一点对称

假设$P_{1\sim 4}$是对称的, 即$P_{1\sim 2} = P_{3\sim 4}$. 如下图:

这个时候我们能不能利用这个$P$的信息做点优化呢? 例如恰好$S$与$P$在$P_5$处失配:

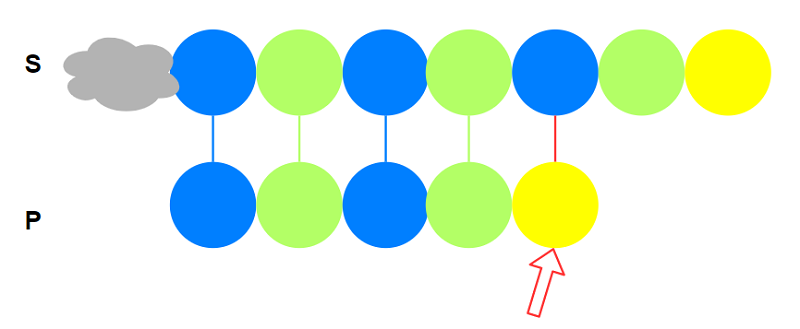
• 以$S_i$作为起点与$P$在$P_5$处失配

• 以$S_i$作为起点与$P$部分匹配: $S_{i\sim i+3}$与$P_{1\sim 4}$匹配.

也就是说我们额外获得信息: $S_{i+2\sim i+3} = P_{3\sim 4}$, 而$P_{1\sim 2} = P_{3\sim 4}$,
所以自然有$S_{i+2\sim i+3} = P_{1\sim 2}$. 因为匹配失败, 所以不能以$S_i$作为起点, 但从
我们获得的信息可以以$s_{i+2}$作为新的起点.

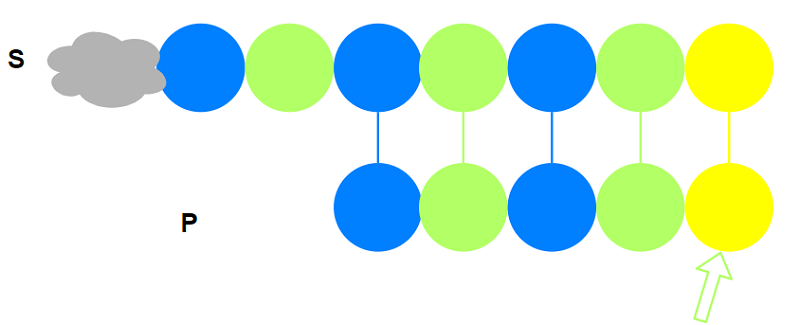
而上面优化的思路再更进一步(也许是好多步), 就来到了我们的 KMP 算法.

KMP $O(m)$

为理解 KMP , 我们需要理解两点:

• 匹配失败时采取的策略

• $P$的额外信息具体是什么, 以及如何计算

1.

为理解$P$的额外信息, 首先需要了解几个概念:

• 真前缀: 字符串从最左侧开始的连续字串(不包含自身). 如abbc的真前缀: a, ab, abb.

• 真后缀: 字符串从最右侧开始的连续字串(不好含自身). 如abbc的真后缀: c, bc, bbc.

• 前缀函数: 一个字符串中相等的真前缀和真后缀中的最长字串的长度. 如ababa的前缀函数为$3$:aba-aba.

2.

实际上对$P$我们需要获取的额外信息为: 以$P{1\sim i}$作为一个字符串, 其前缀函数的值. 其中$1\le i\le n$.

而KMP的策略是: 在匹配到$P_{j+1}$失败, 则以$P_{1\sim j}$作为一个字符串, 将其真前缀移动到其真后缀
的位置.

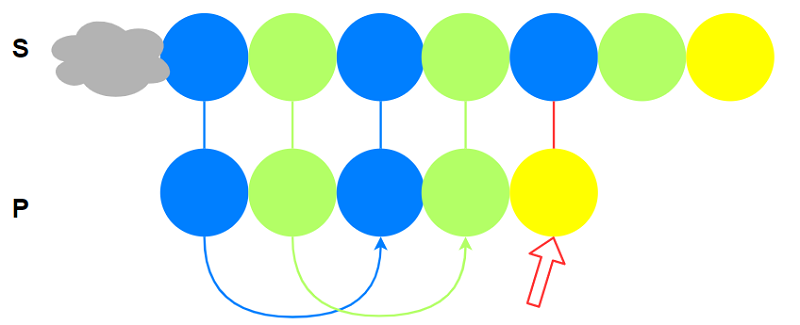
通过跳过绝对不可能匹配的位置以减少匹配次数.

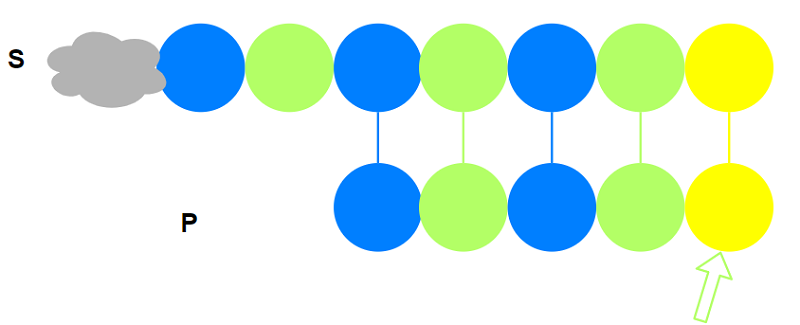
小结

实际上上述过程就是KMP的核心思路, 每次匹配失败kmp都毫不气馁, 而是尽快找到下一个有可能
匹配成功的位置. 每次都从$S$字符串新的位置作为新的开始, 判断真后缀的下一个字符是否能成功.

代码实现

1.

首先考虑失败时策略是如何实现的. 上述的前缀函数体现为$nxt$数组 :

    for( int i = 1, j = 0; i <= m; i ++ )
    {
        while( j && p[j + 1] != s[i] )  j = nxt[j]; //匹配失败
        if( p[j + 1] == s[i] )  j ++;   //尝试下一个位置
        if( j == n )//匹配成功
        {
            //success
            j = nxt[j]; //匹配下一个
        }
    }

其中$P_{1\sim j}$是已经匹配的位置, 首先判断下一个位置能否成功匹配, 若不能则找下一个可能的位置.
上述过程持续至找到下一个可能的位置或$j$退回到$0$. 如果下一个位置能匹配, $j$移动至成功匹配的位置.
如果最后$j$移动至$P$的末尾, 匹配成功, 进行下一次匹配.

2.

考虑如何计算$nxt$数组. 首先考虑更清楚地说明对于$P$, 其$nxt$的含义:

• $nxt_i = j$: $P_{1\sim j} = P_{i - j + 1\sim i}$. 且这里的$j$是满足等式的最大值.

接着考虑KMP的计算过程: 若某次while循环$j$的值为$k$, 则说明此时$S_{i-k+1\sim i} = P_{1\sim k}$.
且此时$k$是满足等式的最大值.

• 我们用$P_{2\sim n}$(作为$S$文本串)与$P_{1\sim n-1}$(作为$P$模式串)进行KMP的匹配过程.
  那么每次获得的值就是$nxt$计算的值.

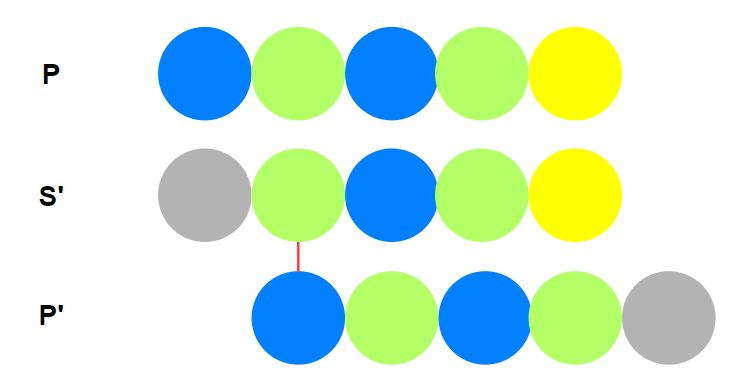
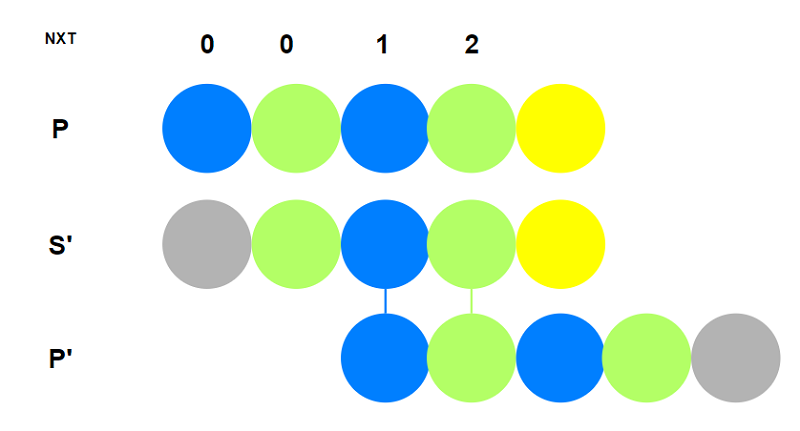
按照上述思路可以编写代码:

    //计算nxt[]
    for( int i = 2; i <= n; i ++ )   s1[i - 1] = p[i]; //s1: p{2~n}
    for( int i = 1; i < n; i ++ )    p1[i] = p[i];  //p1: p{1~n-1}

    for( int i = 1, j = 0; i < n; i ++ )
    {
        while( j && p1[j + 1] != s1[i] )    j = nxt[j];
        if( p1[j + 1] == s1[i] )    j ++ ;
        nxt[i + 1] = j; //因为s[i+1] = p[i], 这里计算的是p的nxt数组
    }

当然我们可以在$P$数组上直接计算, 只要$i$从$2$开始$j$从$1$开始即达到同样效果.

实现代码:

#include <iostream>

using namespace std;

const int N = 1e5 + 10, M = 1e6 + 10;

int n, m;
char p[N], s[M];
int nxt[N];

int main()
{
    cin >> n >> (p + 1) >> m >> (s + 1);

    //计算nxt
    for( int i = 2, j = 0; i <= n; i ++ )
    {
        while( j && p[j + 1] != p[i] )  j = nxt[j];
        if( p[j + 1] == p[i] )  j ++ ;
        nxt[i] = j;
    }

    //kmp
    for( int i = 1, j = 0; i <= m; i ++ )
    {
        while( j && p[j + 1] != s[i] )  j = nxt[j];
        if( p[j + 1] == s[i] )  j ++ ;
        if( j == n )
        {
            cout << i - n << ' ';
            j = nxt[j]; //下一次匹配
        }
    }

    return 0;
}