算法提高课汇总

算法思路

理解题意

相比于AcWing 1057. 股票买卖 IV, 本题少了交易次数而多了冷冻期一天的限制—需要对不持有
股票做进一步划分.

状态机模型

• 状态: 持有股票、不持有股票的第1天(冷冻期)、不持有股票超过1天(可以购入股票).

• 入口: 考虑到初始就可以选择是否购买股票, 所以入口为状态2.

用0表示持有股票、1表示持有股票的第1天、2表示持有股票超过1天. 状态机如图:

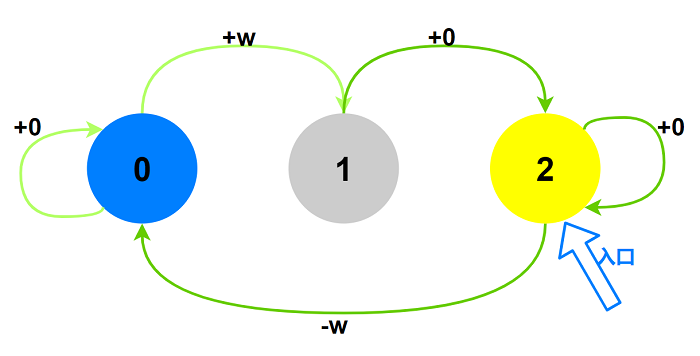
$DP$分析

状态定义$dp(i,0/1/2)$

• 集合: $dp(i, j)$—从入口出发路径长度为$i$, 最终状态为$j$的所有路径. $j\in [0, 2]$.

• 属性: Max

状态计算

依据当前状态从何而来:

• $dp(i, 0) = max\lbrace dp(i - 1, 0), dp(i - 1, 2) - w_i\rbrace$

• $dp(i, 1) = dp(i - 1, 0) + w_i$

• $dp(i, 2) = max\lbrace dp(i - 1, 1), dp(i - 1, 2)$

代码实现

• 初始化: 入口为合法状态, 置为$0$; 非入口置为$-\infty$.

• 出口: 最终应该完成了完整的交易, 即最后状态为不持有股票: $dp(n, 1)/dp(n, 2)$.

具体代码:

#include <iostream>

using namespace std;

const int N = 1e5 + 10, INF = 2e9;

int n;
int w[N];
int dp[N][3];

int main()
{
    cin >> n;
    for( int i = 1; i <= n; i ++ )  cin >> w[i];

    dp[0][0] = dp[0][1] = -INF;
    dp[0][2] = 0;
    for( int i = 1; i <= n; i ++ )
    {
        dp[i][0] = max( dp[i - 1][0], dp[i - 1][2] - w[i] );
        dp[i][1] = dp[i - 1][0] + w[i];
        dp[i][2] = max( dp[i - 1][2], dp[i - 1][1] );
    }
    cout << max( dp[n][1], dp[n][2] ) << endl;

    return 0;
}