双链表

双链表概述

单链表只有一个$next$指针，当前结点可以通过它访问下一个结点。但下一个结点无法访问它。
双链表支持双向访问，每一个结点有两个指针域，一个指向上一个结点，一个指向下一个结点

1. 双链表的表示

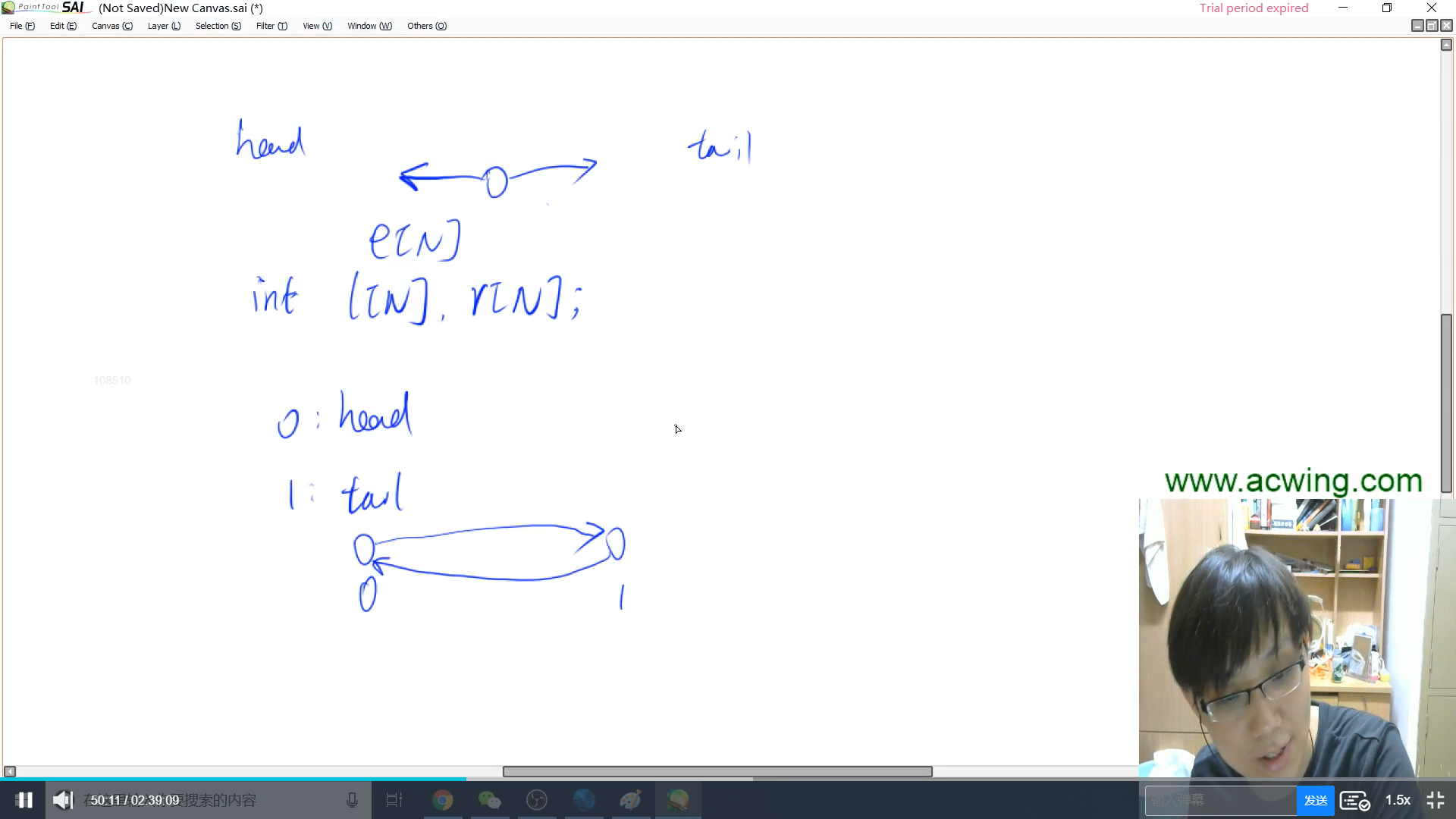
$e$[ ]表示节点的值，$l$[ ]表示节点的左指针，$r$[ ]表示节点的右指针，$idx$表示当前可用结点

int e[N], l[N], r[N], idx;

2. 双链表的初始化

这里我们采用两个哨兵结点来表示左右端点，$1$是左端点，$0$是右端点
由于$0$和$1$已经被使用过了，所以$idx$是从2开始的

void init()
{
    r[0] = 1, l[1] = 0;
    idx = 2;
}

3. 操作

(1) 在节点a的右边插入一个数x

首先，对该节点赋值
其次，调整该结点的左右指针，该节点的右指针指向结点$a$的右边，该结点的左边指向$a$
最后，调整该节点的左右结点，原来$a$的下一个结点的左边是该节点，$a$的右边也该指向该结点

void insert(int a, int x)
{
    e[idx] = x;
    l[idx] = a, r[idx] = r[a];
    l[r[a]] = idx, r[a] = idx ++ ;
}

(2) 删除

依旧采用懒惰删除（实际上空间没有释放，但是正常合法的访问中访问不到它）
让该结点左侧的右指针指向该结点的右侧，该节点右侧的左指针指向该结点的左侧
最后效果是该结点悬空，也就是被删除掉了

// 删除节点a
void remove(int a)
{
    l[r[a]] = l[a];
    r[l[a]] = r[a];
}

本题分析

本题描述有五个操作，但其实只有两个操作，其余都可以向这两个转换
即上面描述的，删除某个结点的结点，以及在某个结点右边插入一个新的结点
本题中，第k个插入的数对应的下表是$k - 1$

操作1：在最左侧插入一个数， 等价于在0的右边插入一个新结点
操作2：在最右侧插入一个数，等价于在1左边的数的右边插入新结点
操作3：将第 k 个插入的数删除，即删除下标为$k + 1$的数
操作4：在第 k 个插入的数左侧插入一个数，等价于在k左边的数的右边插入新结点
操作5：在第 k 个插入的数右侧插入一个数

代码

#include <iostream>

using namespace std;

const int N = 100010;

int m;
int e[N], l[N], r[N], idx;

// 在节点a的右边插入一个数x
void insert(int a, int x)
{
    e[idx] = x;
    l[idx] = a, r[idx] = r[a];
    l[r[a]] = idx, r[a] = idx ++ ;
}

// 删除节点a
void remove(int a)
{
    l[r[a]] = l[a];
    r[l[a]] = r[a];
}

int main()
{
    cin >> m;

    // 0是左端点，1是右端点
    r[0] = 1, l[1] = 0;
    idx = 2;

    while (m -- )
    {
        string op;
        cin >> op;
        int k, x;
        if (op == "L")
        {
            cin >> x;
            insert(0, x);
        }
        else if (op == "R")
        {
            cin >> x;
            insert(l[1], x);
        }
        else if (op == "D")
        {
            cin >> k;
            remove(k + 1);//注意第k个插入的数的下标是k + 1
        }
        else if (op == "IL")
        {
            cin >> k >> x;
            insert(l[k + 1], x);
        }
        else
        {
            cin >> k >> x;
            insert(k + 1, x);
        }
    }

    for (int i = r[0]; i != 1; i = r[i]) cout << e[i] << ' ';
    cout << endl;

    return 0;
}