算法提高课汇总

算法思路

理解题意

1. 限制

   • 不能连续买入/卖出股票
   • 交易次数(买入和卖出合为一次交易)

2. 目的

   • Max利润

本题在类似AcWing 1049. 大盗阿福的题意的基础上, 限制了状态交替的次数.

状态机模型

• 状态定义: 这里巧妙的没有直接将状态定义为买入/卖出股票, 否则状态必须交替, 因为两次连续
  买入是不合法的; 这里状态定义为持有股票/不持有股票.

• 有向边表示每天的决策, 权重表示此次决策收益.

• 一条路径的长度表示天数; 而购买股票的次数体现为两个状态交替的次数.

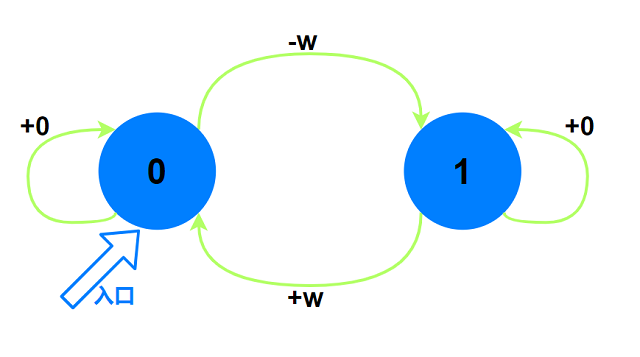
我们用0:不持有股票; 1表示持有股票. 状态机如图:

$DP$分析

按之前的$DP$思路本题的状态定义应为: $dp(i, j)$—前$i$天且购买股票$j$次的所有方案. 而状态机模型
在此基础上对其进行了细分, 多出的状态简化我们的分析过程.

这里还需考虑何时更新股票交易次数这个状态,而我们不能一次考虑买入和卖出. 由于入口为0
(初始合法状态为不持有股票),所以我们用一次0到1的状态交替作为股票次数的更新.

状态定义$dp(i, j, 0)$/$dp(i, j, 1)$

• 集合: $dp(i, j, k)$—从起点出发路径长度为$i$、状态从0到1的次数为$j$、最终状态为$k$的所有路径. $k\in [0, 1]$.

• 属性: Max股票利润

状态计算

依据状态从哪些状态转移过来.

• $dp(i, j, 0) = max\lbrace dp(i - 1, j, 0), dp(i - 1, j, 1) + w_i\rbrace$.

• $dp(i, j, 1) = max\lbrace dp(i - 1, j, 1), dp(i - 1, j - 1, 0) - w_i\rbrace$. 这里从0到1购买股票
  的次数会更新.

代码实现

初始化

初始化的目的: 让初始时不合法状态不会更新后续状态; 让初始合法状态更新后续状态.

本题中$dp(i, 0, 0) = 0, 0\le i\le n$—从入口走自环$i$次即保持不持有股票; 其他状态都可设为不合法,
因本题求最大可以设为$-\infty$.

最终解的计算

状态的起点为$dp(i, 0, 0)$, 终点为$dp(n, j, 0)$.

具体代码

#include <cstring>
#include <iostream>

using namespace std;

const int N = 1e5 + 10, M = 110;

int n, m;
int w[N];
int dp[N][M][2];

int main()
{
    cin >> n >> m;
    for( int i = 1; i <= n; i ++ )  cin >> w[i];

    memset(dp, -0x3f, sizeof dp);
    for( int i = 0; i <= n; i ++ )  dp[i][0][0] = 0;

    for( int i = 1; i <= n; i ++ )
    {
        for( int j = 1; j <= m; j ++ )
        {
            dp[i][j][1] = max( dp[i - 1][j][1], dp[i - 1][j - 1][0] - w[i] );
            dp[i][j][0] = max( dp[i - 1][j][0], dp[i - 1][j][1] + w[i] );
        }
    }

    int res = 0;
    for( int j = 1; j <= m; j ++ )  res = max( res, dp[n][j][0] );
    cout << res << endl;

    return 0;
}