算法提高课汇总

算法思路

理解题意

1. 限制
   • 条件限制: 不能连续选择物品
2. 目标
   • Max物品价值

相比于$01$背包, 限制条件从物品的体积变为一个条件限制: 不能连续选择物品,也就是我们此时需要
关注物品$i$是否被选. 原本限制体积的状态在本题中用于表示是否选择.可以用状态机模型清晰的表示
不同状态间的关系.

状态机模型

状态机: 用一些确定的状态及状态间的关系描述一个过程.

本题中需要表示第$i$个物品选/不选两种状态, 且不能连续选择. 状态间的关系如图:

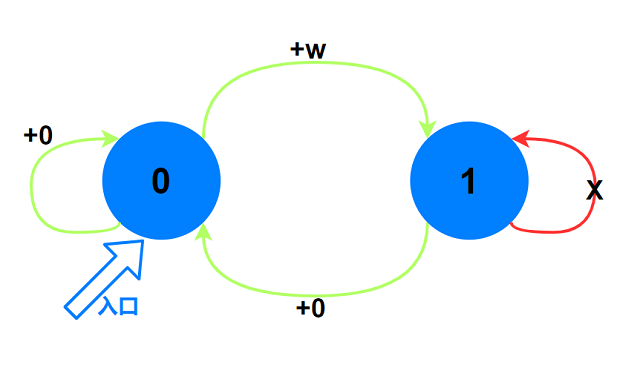
上图具体含义:

• 状态: 用0和1分别表示选/不选.

• 有向边: 表示下一个物品选/不选, 每条边表示一次决策; 边权表示这次决策的收益.

• 阿福的一种选择与图中长度为$N$的一条路径一一对应.

依照状态机模型我们就很容易做$DP$分析了.

$DP$分析

状态表示 $dp(i, 0)$/$dp(i, 1)$

• 集合: $dp(i, j)$表示所有走了$i$步且最终状态为$j$的路径. $j\in [0, 1]$.

• 属性: Max

状态计算

依据最后一步的选择, 在状态机模型中对应当前状态从何而来:

• $dp(i, 0)$: 其上一个状态可以是$dp(i - 1, 0)$/$dp(i - 1, 1)$, 且对应边的权重均为0.
  有$dp(i, 0) = max\lbrace dp(i - 1, 0), dp(i - 1, 1)\rbrace$.

• $dp(i, 1)$: 其上一个状态只能是$dp(i - 1, 0)$. 且对应边的权重为$w_i$, 即物品$i$的价值,
  有$dp(i, 1) = dp(i - 1, 0) + w_i$.

因为阿福的每个决策都与图中长度为$N$的路径一一对应, 所以$DP$的计算过程相当于将所有路径的可能都
计算了一遍.

代码实现

• 初始化: 初始(可以认为是第$0$个物品)没有物品可选, 所以只有状态$0$合法.

具体代码:

#include <iostream>

using namespace std;

const int N = 1e5 + 10, INF = 0x3f3f3f3f;

int n;
int w[N], dp[N][2];

int main()
{
    int T;
    scanf("%d", &T);
    while( T -- )
    {
        scanf("%d", &n);
        for( int i = 1; i <= n; i ++ )  scanf("%d", &w[i]);

        dp[0][0] = 0; dp[0][1] = -INF;
        for( int i = 1; i <= n; i ++ )
        {
            dp[i][0] = max( dp[i - 1][0], dp[i - 1][1] );
            dp[i][1] = dp[i - 1][0] + w[i];
        }

        printf("%d\n", max( dp[n][0], dp[n][1]) );
    }

    return 0;
}