算法提高课汇总

算法思路

题意理解

不同于买书—求物品体积恰好为$m$的方案数, 本题求构成最优解的方案数.

$DP$分析

可以用求最短路径的条数的相同思路: 从起点到当前节点最短路径的个数为所有到达该点为最短路
的对应的状态的路径个数之和.

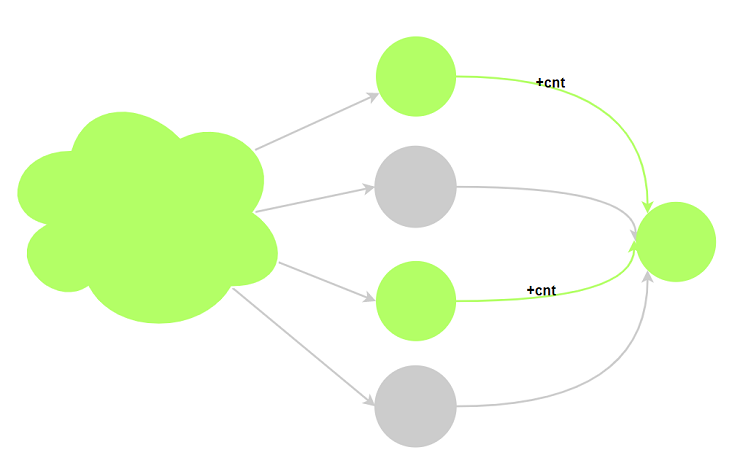
关于$01$背包状态的分析可参考🔗. 这里主要分析方案数的状态.

状态定义 $cnt(i, j)$

集合: $dp(i, j)$计算完毕后对应状态的方案数.

属性: Count

状态计算

$cnt(i, j) = \sum_{k}cnt(i - 1, k)$.其中$k$满足$dp(i,j) == dp(i - 1, k)$

直观理解: 以$01$背包为例:

• 如果$dp(i, j) == dp(i - 1, j)$, 即不选物品$i$即有最优解, 那么我们可以沿用$dp(i - 1, j)$的所有方案

• 如果$dp(i, j) == dp(i - 1, j - v_i) + w_i$, 则选择物品$i$, 此时的方案是在$dp(i - 1, j - v_i)$的所有
  方案的最后加上物品$i$.

• 如果二者均满足则取其和即可. 对于其他问题思路相同.

算法实现

这里关于$dp(i, j)$的定义可以是体积不超过$j$或体积恰好为$j$. 区别在于初始化和最后方案数的统计.

初始化:

• 不超过: $dp(0, i), 0\le i\le m$均为合法状态. 所以$cnt(0, i) = 1$, 即方案—啥都不选.

• 恰好: $dp(0, 0) = 0$为初始唯一合法状态. 所以初始$cnt(0, 0) = 1$. 其他均为$0$.

方案统计:

• 不超过: 最优解为$dp(n, m)$, 所有情况都考虑完毕, 所以对应方案数为$cnt(n, m)$.

• 恰好: 最优解为$dp(n, k) == maxv$, 即最优解体积不确定且可能有多个, 需要将所有最优解状态的方案数求和.

不超过; 二维空间

#include <iostream>

using namespace std;

const int N = 1010, M = 1010, mod = 1e9 + 7;

int n, m;
int v[N], w[N];
int dp[N][M], cnt[N][M];

int main()
{
    cin >> n >> m;
    for( int i = 1; i <= n; i ++ )  cin >> v[i] >> w[i];

    for( int i = 0; i <= m; i ++ )  cnt[0][i] = 1;//初始化
    for( int i = 1; i <= n; i ++ )
    {
        for( int j = 0; j <= m; j ++ )
        {
            dp[i][j]  = dp[i - 1][j];
            cnt[i][j] = cnt[i - 1][j]; //不选物品i的方案数
            if( j >= v[i] )
            {
                if( dp[i][j] < dp[i - 1][j - v[i]] + w[i] )
                {//选择物品i才是最佳选择
                    dp[i][j]  = dp[i - 1][j - v[i]] + w[i];
                    cnt[i][j] = cnt[i - 1][j - v[i]];
                }
                else if( dp[i][j] == dp[i - 1][j - v[i]] + w[i] )
                {//选/不选物品i都是最优方案
                    cnt[i][j] = ( cnt[i][j] + cnt[i - 1][j - v[i]] ) % mod;
                }
            }
        }
    }
    cout << cnt[n][m] << endl;

    return 0;
}

不超过; 一维空间

#include <iostream>

using namespace std;

const int N = 1010, M = 1010, mod = 1e9 + 7;

int n, m;
int v[N], w[N];
int dp[M], cnt[M];

int main()
{
    cin >> n >> m;
    for( int i = 1; i <= n; i ++ )  cin >> v[i] >> w[i];

    for( int i = 0; i <= m; i ++ )  cnt[i] = 1;//初始化
    for( int i = 1; i <= n; i ++ )
    {
        for( int j = m; j >= v[i]; j -- )
        {
            if( dp[j] < dp[j - v[i]] + w[i] )
            {//选择物品i是最优方案
                dp[j]  = dp[j - v[i]] + w[i]; 
                cnt[j] = cnt[j - v[i]];
            }
            else if( dp[j] == dp[j - v[i]] + w[i] )
            {//选/不选物品i都是最优方案
                cnt[j] = ( cnt[j] + cnt[j - v[i]] ) % mod; 
            }
        }
    }
    cout << cnt[m] << endl;

    return 0;
}

恰好; 二维

#include <cstring>
#include <iostream>

using namespace std;

const int N = 1010, M = 1010, mod = 1e9 + 7;

int n, m;
int v[N], w[N];
int dp[N][M], cnt[N][M];

int main()
{
    cin >> n >> m;
    for( int i = 1; i <= n; i ++ )  cin >> v[i] >> w[i];

    //初始化
    cnt[0][0] = 1;
    memset(dp, -0x3f, sizeof dp);
    dp[0][0] = 0; //初始唯一合法状态
    for( int i = 1; i <= n; i ++ )
    {
        for( int j = 0; j <= m; j ++ )
        {
            dp[i][j]  = dp[i - 1][j];
            cnt[i][j] = cnt[i - 1][j]; //不选物品i的方案数
            if( j >= v[i] )
            {
                if( dp[i][j] < dp[i - 1][j - v[i]] + w[i] )
                {//选择物品i才是最佳选择
                    dp[i][j]  = dp[i - 1][j - v[i]] + w[i];
                    cnt[i][j] = cnt[i - 1][j - v[i]];
                }
                else if( dp[i][j] == dp[i - 1][j - v[i]] + w[i] )
                {//选/不选物品i都是最优方案
                    cnt[i][j] = ( cnt[i][j] + cnt[i - 1][j - v[i]] ) % mod;
                }
            }
        }
    }

    int maxv = 0, res = 0;
    for( int i = 0; i <= m; i ++ )  maxv = max( maxv, dp[n][i] );
    for( int i = 0; i <= m; i ++ )
        if( dp[n][i] == maxv )
            res = ( res + cnt[n][i] ) % mod;
    cout << res << endl;

    return 0;
}

恰好; 一维

#include <cstring>
#include <iostream>

using namespace std;

const int N = 1010, M = 1010, mod = 1e9 + 7;

int n, m;
int v[N], w[N];
int dp[M], cnt[M];

int main()
{
    cin >> n >> m;
    for( int i = 1; i <= n; i ++ )  cin >> v[i] >> w[i];

    //初始化
    cnt[0] = 1;
    memset(dp, -0x3f, sizeof dp);
    dp[0] = 0; //初始唯一合法状态
    for( int i = 1; i <= n; i ++ )
    {
        for( int j = m; j >= v[i]; j -- )
        {
            if( dp[j] < dp[j - v[i]] + w[i] )
            {//选择物品i才是最佳选择
                dp[j]  = dp[j - v[i]] + w[i];
                cnt[j] = cnt[j - v[i]];
            }
            else if( dp[j] == dp[j - v[i]] + w[i] )
            {//选/不选物品i都是最优方案
                cnt[j] = ( cnt[j] + cnt[j - v[i]] ) % mod;
            }
        }
    }

    int maxv = 0, res = 0;
    for( int i = 0; i <= m; i ++ )  maxv = max( maxv, dp[i] );
    for( int i = 0; i <= m; i ++ )
        if( dp[i] == maxv )
            res = ( res + cnt[i] ) % mod;
    cout << res << endl;

    return 0;
}

这里恰好和不超过的定义方式在状态计算的分析过程相同. 区别仅在初始化和方案数统计. 而空间
的优化即代码的简单等价变形, 方式与普通$01$背包的优化方式一致.