算法提高课汇总

算法思路

理解题意

1. 限制
   • 物品容量$v$
   • 条件限制: 选择某节点的必要条件是选择其父节点
2. 目的
   • Max物品价值

物品间的依赖关系构成树形, 类似AcWing 285. 没有上司的舞会. 不同点在于本题的选择是“连续”的.

我们用蓝色表示选, 灰色表示不选, 用一个例子表明“连续”选择的含义:

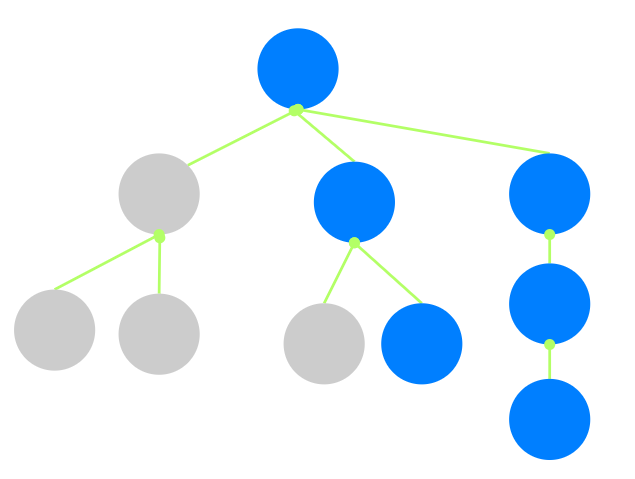
本题也可看作是AcWing 487. 金明的预算方案的扩展, 不同点在于金明的预算方案中依赖关系比较简单,
且依赖的物品数量小, 所以可以枚举所有依赖物品的选法. 而本题以节点$i$为根的子树其所有子节点数目
较大, 如果用二进制枚举会超时. 这里的思路是用子集的体积作为划分依据而不是子集中物品的选择,
时间复杂度从$2^k \rightarrow m + 1$.($k$: 子集物品数目; $m$: 总体积).

$DP$分析

状态表示 $dp(u, i, j)$

• 集合: 从以$u$为根的子树中选前$i$个孩子节点, 且总体积不超过$j$的所有方案
  由于问题是树形的而不是线性的, 这里的$i$不是物品的编号而是决策的顺序, 本质上是相同的.

• 属性: Max物品价值

状态计算

对于没有依赖的背包问题我们考虑的是第$i$个物品的选择和对应前$i - 1$个物品的状态.
树形$DP$我们考虑的是当前物品和其孩子节点的选择和对应的状态.

我们可以每次将以$i$为根的子树的直接孩子节点作为物品组, 即每个子节点作为一组物品, 而组内的选择
根据状态定义不是物品的决策, 而是分配的体积. 此时可以按分组背包 的思路思考.

也就是在树形$DP$的框架下我们只需考虑当前$i$节点和其子节点; 而所有对所有子节点的决策并不是选择
的数量而是分配的体积, 如果将子节点作为物品组、体积作为物品组内的互斥决策, 那么问题可以看作分组
背包问题. 此外为满足本题的依赖条件, 必须选择物品$i$, 否则其子树节点全不能选.

分组背包的状态计算:

$\;\;\;\;dp(i, j) = max\lbrace dp(i - 1, j - v_{ik}) + w_{ik}\rbrace$, $k\in [0, s_i]$

类似的,

$\;\;\;\;dp(u, i, j) = max\lbrace dp(u, i - 1, j - k) + dp(son, size_{son}, k)\rbrace, k\in [0, m]$

其中$dp(u, \cdot , \cdot)$表明以节点$u$为根节点的子树作为单个分组背包问题考虑; $i$表明考虑到第$i$个子节点,
而$k$作为决策—分配的体积; $f[son][size_{son}][k]$作为决策的收益. 其中$size_{son}$为$son$节点子节点的个数.

理解$size_{son}$: 分组背包问题最后输出$dp(n,m)$, $size_{son}$即$son$节点遍历其所有子节点后的状态.

代码实现 $O(NV^2)$

这里相比无依赖的多重背包需要注意:

• 树形$DP$: 先计算子节点状态再计算父节点

• 依赖条件: 对于$dp(u, i, j)$必须选择节点$u$, 否则子节点都不能选择; 由于体积限制不能选$u$的
  状态的值需要设为$0$.

具体实现时实际上状态定义为$dp(u, j)$, 也即优化空间后的分组背包问题. 下面是我对几个代码问题的理解:

• 为什么先计算分配子节点体积的状态最后计算加入节点$u$的状态 ?
  个人觉得这里仍然是树形$DP$的思路: 先计算子节点状态再计算当前节点. 不过不同于没有依赖的
  树形$DP$:可以计算完子节点状态后在当前节点直接使用子节点的状态, 本题需要在当前节点计算其
  直接子节点的状态.原因是子节点的状态与当前节点状态对应的是两个分组背包问题.(这里只是我的理解)

• 为什么分配子节点状态从$m - v_u$开始: 由于依赖关系$u$必须选择, 所以$m\sim j - v_u + 1$的
  状态对于子节点是不合法的.

• 本质来说, 状态计算过程中$ + dp(son, k)$和$ + w[u]$都是剩余状态的收益.

具体代码:

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110, M = 110;

int n, m;
int v[N], w[N];
int dp[N][M];
int h[N], e[N], ne[N], idx;

void add(int u, int v)
{
    e[idx] = v, ne[idx] = h[u], h[u] = idx ++;
}

void dfs( int u )
{
    for( int i = h[u]; ~i; i = ne[i] )
    {//物品组
        int son = e[i];
        dfs( son ); //首先计算子节点状态

        for( int j = m - v[u]; j >= 0; j -- )
        {//体积, 即dp(u, i, j)先枚举状态 不过这里的i是枚举物品的顺序 不是循环变量i
            for( int k = 0; k <= j; k ++ )
            {//决策, 这里是分配的体积
                dp[u][j] = max( dp[u][j], dp[u][j - k] + dp[son][k] ); 
            }
        }
    }

    for( int j = m; j >= v[u]; j -- )   dp[u][j] = dp[u][j - v[u]] + w[u];//最后加上当前节点u
    for( int j = 0; j < v[u]; j ++ )   dp[u][j] = 0; //由于依赖关系的限制

}

int main()
{
    cin >> n >> m;

    memset(h, -1, sizeof h);
    int root;
    for( int i = 1; i <= n; i ++ )
    {
        int p;
        cin >> v[i] >> w[i] >> p;
        if( p == -1 )   root = i;
        else    add(p, i);
    }

    dfs( root );
    cout << dp[root][m] << endl; //以整个树作为分组背包问题求解

    return 0;
}

关于本题个人由于水平理解还有些欠缺, 之后会更新思路. 个人觉得关键注意两点:

1. 对于$dp(u, i, j)$的理解

2. 每个$dp(u, \cdot)$都是一个分组背包问题