算法思路
理解题意
-
限制
- 每个职员👨💼可选择出席
/不出席 - 条件依赖: 职员不能和其上司共同出席
- 每个职员👨💼可选择出席
-
目的
Max幸福度
从职员节点向其上司建一条边, 则$N$名职员的关系可以看作是一颗树. 而条件限制为选择子节点的
必要条件是不选其父节点. 我们可以按从父到子节点的递归顺序考虑是否选择.
$DP$分析
状态机模型
实际上本题可以看作是状态机模型: 每个节点都有两种状态—选/不选. 如果选, 那么其所有子节点都
不能被选; 如果不选, 则其子节点状态任意.
我们用蓝色表示选择, 灰色表示不选.
若选择节点$i$, 则其所有子节点的状态均为不选:
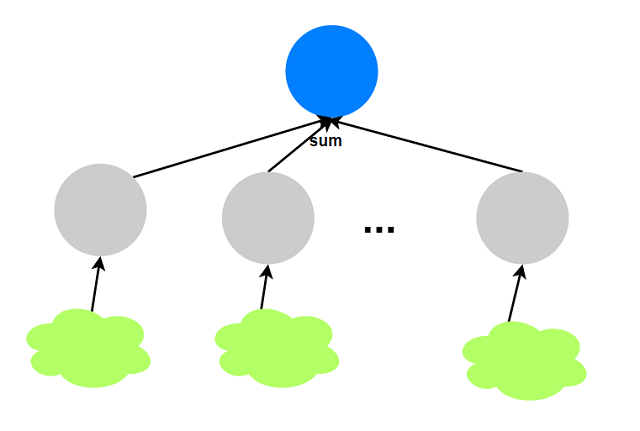
若不选节点$i$, 则其所有子节点状态任意, 取每个子节点2个状态的较大值:
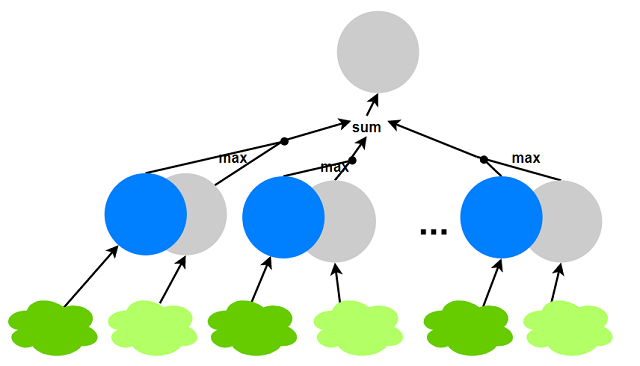
状态定义 $dp(i, 0)、dp(i, 1)$
-
集合: 从以$i$为根的树中选, 且不选($0$)
/选($1$)节点$i$的所有选法 -
属性:
Max快乐指数
状态计算
-
选$i$, 所有子节点状态确定: $dp(son, 0)$. $dp(i, 1) = \sum_{j}dp(son_j, 0) + w_i$
-
不选$i$, 所有子节点状态任意, 取较大值. $dp(i, 0) = \sum_{j} max\lbrace dp(son_j, 0), dp(son_j, 1)\rbrace$
代码实现
状态转移次数等价于树的边数, 每个状态计算时间为常数级, 所以时间复杂度为$O(N)$.
#include <cstring>
#include <iostream>
using namespace std;
const int N = 6010;
int n;
int w[N];
int dp[N][2];
int h[N], e[N], ne[N], idx; //用邻接表保存树
bool st[N]; //st[i] = true表示节点i有父节点. st[i] = false表明i为根
void add(int u, int v)
{
e[idx] = v, ne[idx] = h[u], h[u] = idx ++ ;
}
void dfs( int u )
{
//dp[u][0] = 0
dp[u][1] = w[u];
for( int i = h[u]; ~i; i = ne[i] )
{
int son = e[i];
dfs( son ); //首先计算子节点的所有状态
dp[u][1] += dp[son][0];
dp[u][0] += max( dp[son][0], dp[son][1] );
}
}
int main()
{
cin >> n;
for( int i = 1; i <= n; i ++ ) cin >> w[i];
memset(h, -1, sizeof h);
for( int i = 1; i < n; i ++ )
{
int a, b;
cin >> a >> b;
add(b, a);
st[a] = true;
}
int root;
for( root = 1; ; root ++ ) if( !st[root] ) break;
dfs( root );
cout << max( dp[root][0], dp[root][1] ) << endl;
return 0;
}

