算法提高课汇总

算法思路

求背包问题的具体方案实际上就是求最优解的集合—对于$01$背包问题也即最优解中每个物品是否被选.

判断物品$i$是否被选

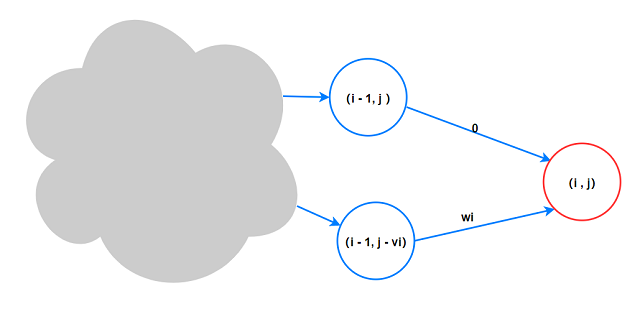
观察$01$背包问题的递推式:

$\;\;\;\;dp(i, j) = max\lbrace dp(i - 1, j), dp(i - 1, j - v_i) + w_i\rbrace$

$dp(i, j)$会选择两项中较大者, 而前者对应的是不选物品$i$, 后者对应选择. 所以我们是通过$dp(i)$
与$dp(i - 1)$的关系判断$i$是否被选(倒推).

• 求具体方案的问题可以视为最短路的具体路径, 而这里路径的推理是从终点到起点反推得到的.

字典序最小的方案

按照之前求解$01$背包问题的思路, 物品从$1\sim n$依次判断是否选取, 那么图的终点为$dp(n,V)$, 因为
具体方案是反推得到的, 所以我们不能保证一定能得到字典序最小的方案. 这是为什么呢?

• 因为计算过程中对于状态$dp(i, j)$可能出现$dp(i - 1, j) == dp(i - 1, j - v_i) + w_i$的情况, 也就是对于物品$i$选不选都可, 此时为了尽量满足字典序最小我们会不选物品$i$, 但剩余的部分不能保证一定会选择字典序最小方案: 例如问题的最优解为$\lbrace 1, 4\rbrace, \lbrace 2, 3\rbrace$,如果在第4个物品我们选择不选, 那么最后求解出的具体方案是只是$\lbrace 2, 3\rbrace$.

所以正确思路是我们按$n\rightarrow 1$的顺序求解$01$背包问题, 接着按$1\rightarrow n$的顺序反推每个背包是否被选. 此时如果遇到$dp(i + 1, j) == dp(i + 1, j - v_i) + w_i$的情况, 也即对于最优解可以选也可不选$i$, 为了字典序最小我们必选物品$i$.

代码实现

#include <iostream>

using namespace std;

const int N = 1010, M = 1010;

int n, m;
int v[N], w[N];
int dp[N][M];

int main()
{
    cin >> n >> m;
    for( int i = 1; i <= n; i ++ )  cin >> v[i] >> w[i];

    for( int i = n; i >= 1; i -- )
    {
        for( int j = 0; j <= m; j ++ )
        {
            dp[i][j] = dp[i + 1][j];
            if( j >= v[i] ) dp[i][j] = max( dp[i][j], dp[i + 1][j - v[i]] + w[i] );
        }
    }

    int V = m; //图的终点对应状态(1, m). 
    for( int i = 1; i <= n; i ++ )
    {
        if( V >= v[i] && dp[i][V] == dp[i + 1][V - v[i]] + w[i] )
        {//可选, 则为字典序最小, 必选
            cout << i << ' ';
            V -= v[i];
        }
    }

    return 0;
}