最长不重复子序列

双指针算法概述

双指针算法

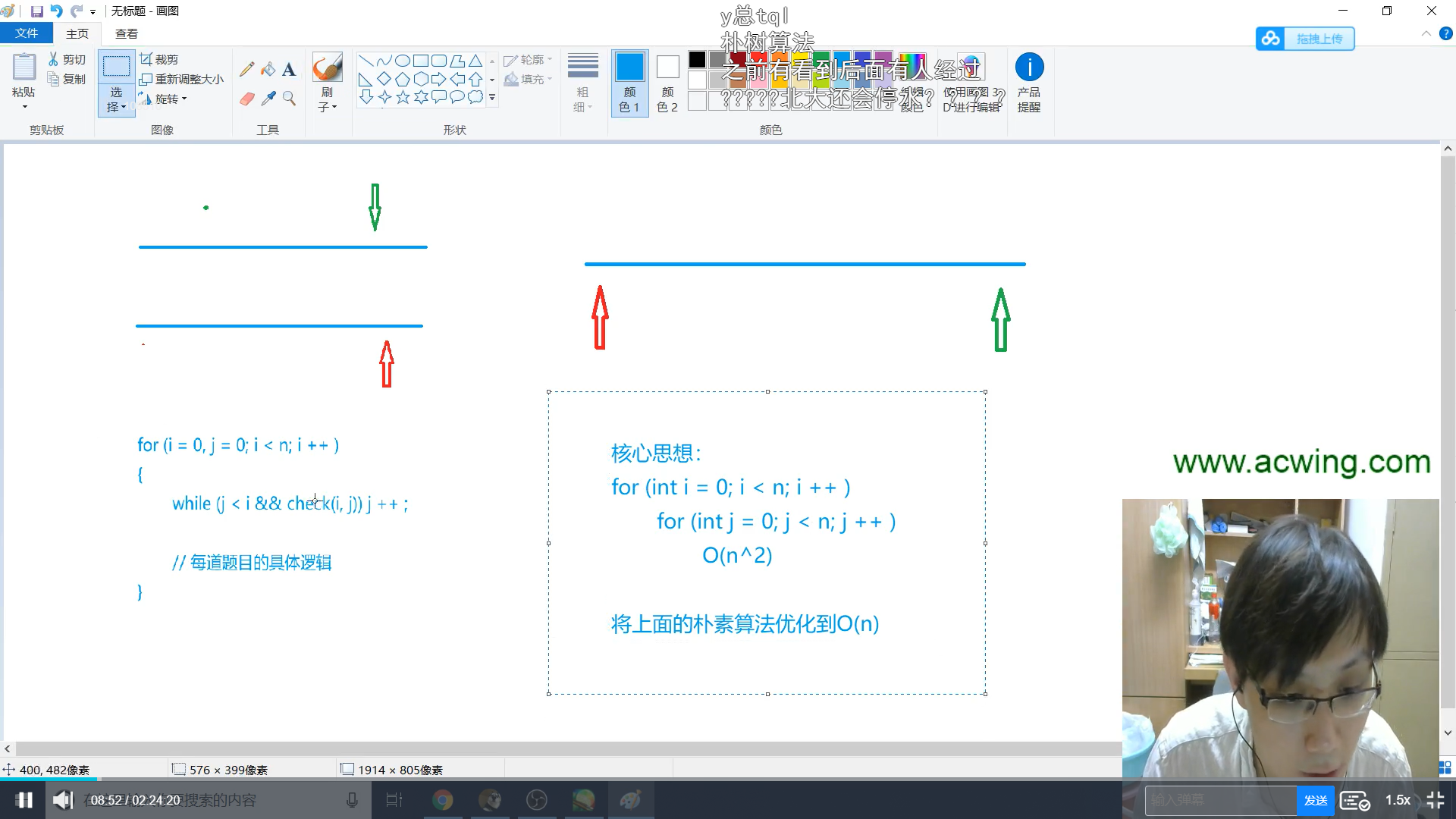
一般双指针问题，我们可以先想出一个暴力的算法，然后如果其中有单调性，那么可以考虑用双指针算法优化。最终可以将一个$O(n^2)$的问题优化到$O(n)$

双指针由快慢指针(同相的两个指针)，或者对撞指针(异相的两个指针)构成

常见问题分类：

$(1)$ 对于一个序列，用两个指针维护一段区间

$(2)$ 对于两个序列，维护某种次序，比如归并排序中合并两个有序序列的操作

双指针算法模板

for (int i = 0, j = 0; i < n; i ++ )
{
    while (j < i && check(i, j)) j ++ ;

    // 具体问题的逻辑
}

本题目分析

1. 暴力做法

以每个数字结尾的最长子序列，我们可以从这个数字想前枚举，直到找到重复元素
最后所有数字结尾的最长取max

2.寻找单调性，利用双指针思想求解

我们可以发现，对于$a[i]$向左最远也远不过$a[i - 1]$向左.这就是单调性，我们可以从左向右依次寻找对于数组中数字向左最远能到达的结点
因此我们可以用双指针算法进行优化

对于数组中的元素，i指针表示当前以$q[i]$结尾，我们依次寻找它向左最远能到达的点
由于此点有单调性，我们用j也是从左向右的移动

每次$i ++$ ，对于$q[i + 1]$，如果$j ~ q[i + 1]$有重复，那么肯定是$q[i + 1]$这个元素重复，$j$右移，知道$q[i + 1]$仅出现一次

移动归位后，区间内没有重复元素，区间内元素个数是$i - j + 1$，此时更新$res$, $res = max(res, i - j + 1)$

本题规模较小，所以数字判重就采用的数组$s[i]$表示，在某段区间，$i$元素出现的次数。如果数据规模较大，可以采用哈希技术，之前学过的离散化也可以处理（离散化是一种特殊的哈希）

时间复杂度分析

虽然有两层，但是我们可以发现$j$最多是遍历一次数组,$i$也是遍历一般数组
所以是$2n$，也就是$O(n)$的时间复杂度

代码

#include <iostream>

using namespace std;

const int N = 100010;

int n;
int q[N], s[N];
// q[N]原数组, s[N]是判重数组
// s[i]表示元素i在区间内出现的次数
int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);

    int res = 0;
    for (int i = 0, j = 0; i < n; i ++ )
    {
        s[q[i]] ++ ;//元素q[i]出现的次数加一
        while (j < i && s[q[i]] > 1) s[q[j ++ ]] -- ; // 当最后一个元素还是重复元素时候, j右移
        res = max(res, i - j + 1); // 区间内无重复元素后，更新答案
    }

    cout << res << endl;

    return 0;
}