算法
(二分) O(n)
为了便于分析,我们先将数组中的数画在二维坐标系中,横坐标表示数组下标,纵坐标表示数值,如下所示:
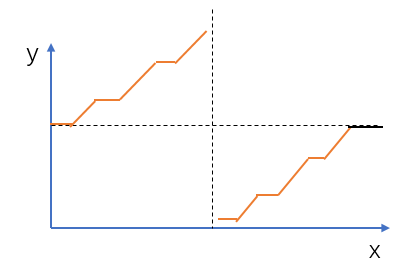
图中水平的实线段表示相同元素。
我们发现除了最后水平的一段(黑色水平那段)之外,其余部分满足二分性质:竖直虚线左边的数满足 nums[i]≥nums[0];而竖直虚线右边的数不满足这个条件。
分界点就是整个数组的最小值。
所以我们先将最后水平的一段删除即可。
另外,不要忘记处理数组完全单调的特殊情况:
- 当我们删除最后水平的一段之后,如果剩下的最后一个数大于等于第一个数,则说明数组完全单调。
时间复杂度分析
二分的时间复杂度是 O(logn),删除最后水平一段的时间复杂度最坏是 O(n),所以总时间复杂度是 O(n)。
C++ 代码
class Solution {
public:
int findMin(vector<int>& nums) {
int n = nums.size() - 1;
if (n < 0) return -1;
while (n > 0 && nums[n] == nums[0]) n -- ;
if (nums[n] >= nums[0]) return nums[0];
int l = 0, r = n;
while (l < r) {
int mid = l + r >> 1; // [l, mid], [mid + 1, r]
if (nums[mid] < nums[0]) r = mid;
else l = mid + 1;
}
return nums[r];
}
};


### 既然都是O(n),那为什么不使用下面的代码😂
class Solution { public: int findMin(vector<int>& nums) { if(!nums.size()) return -1; int ans = INT_MAX; for(int i = 0; i < nums.size(); i ++ ){ ans = min(ans, nums[i]); } return ans; } };它说最坏是0N,你这个遍历的话,所有情况都是0N
class Solution { public: int findMin(vector<int>& nums) { if(nums.empty()) return -1; int n=nums.size()-1; while(n>0&&nums[n]==nums[0]) n--; //单调 if(nums[n]>nums[0]) return nums[0]; int l=0,r=n; while(l<r) { int mid=l+r+1>>1; if(nums[mid]>=nums[0]) l=mid; else r=mid-1; } return nums[r]; } };为啥用二分的另一个模板过不了
用第一个模板就能过
class Solution { public: int findMin(vector<int>& nums) { if(nums.empty()) return -1; int n=nums.size()-1; while(n>0&&nums[n]==nums[0]) n--; //单调 if(nums[n]>nums[0]) return nums[0]; int l=0,r=n; while(l<r) { int mid=l+r>>1; if(nums[mid]<nums[0]) r=mid; else l=mid+1; } return nums[r]; } };第一个模板,不是不过,是你理解错了,在if(nums[mid]>=nums[0]) l=mid; 这个地方不应该更l=mid,应该写l=mid+1,但是这个不符合模板(当if(true) 时 l=mid),所以就要写另一个
第二个应该是 return nums[l];不是return nums[r]
按照二分模版的理解 l 和 r 谁设置成mid 另一个遵循 l = mid +1 r = mid - 1 只需要理解
如果要找的数 大于(r设置为mid)要找的第一个数
如果要找的数 小于(l设置为mid) 要找的最后一个数
上面的模板找的是>=nums[0]的最后一个数, 下面的模板找的是<num[0]的第一个数(本题要找的答案).
可以再看看整数二分的模板题789.数的范围更好地理解划分依据
class Solution { public: int findMin(vector<int>& nums) { // 旋转后的数组是两段分别升序的 if (nums.empty()) return -1; int n = nums.size() - 1; //如果旋转后的数组左半段的开头和右半段的结尾有相同的值,需要去掉右边重复的部分,使其单调 while (n > 0 && nums[n] == nums[0]) n--; //当我们删除最后水平的一段之后,如果剩下的最后一个数大于等于第一个数,则说明数组完全单调。 if (nums[n] > nums[0]) return nums[0]; int l = 0, r = n; while(l < r) { int mid = l + r >> 1; // 如果 nums[mid] < nums[0],说明mid在右半段,要找的最小值在mid的左边 if (nums[mid] < nums[0]) r = mid; //注意这里没有=,自己想一下 // 如果 nums[mid] >= nums[0],说明mid在左半段,要找的最小值在右半段——mid的右边 else l = mid + 1; } return nums[l]; } };如果nums【0】大于当前找到的mid,那不是说明nums【0】本身是个大数,要找到最小值应该在右半部分吗??
是的,可是nums[0]的下标肯定小于等于mid,所以r=mid
class Solution {
public int findMin(int[] nums) {
if(nums.length==0){
return -1;
}else if(nums.length==1){ return nums[0]; } int x=0; int flag=0; for(int i=0;i<nums.length-1;i++){ if(nums[i]>nums[i+1]){ flag=1; x=nums[i+1]; } } if(flag==1) return x; else{ return nums[0]; } }} 面向结果编程哈哈
这代码好难理解
加油hh
后续的啥时候能出呀,都迫不及待了,好多题都不会,网上的都没你讲的清楚(哭唧唧)
暑期的时候hh
感觉这题很简单,为啥是中等难度
class Solution {
public:
int findMin(vector[HTML_REMOVED]& nums) {
if(nums.size() == 0) return -1;
int a = nums[0];
int n = nums.size();
for(int i=0;i[HTML_REMOVED]nums[i]){
return nums[i];
}
}
return nums[0];
}
};
你们都错了,我同学是对的
有两段可重复的有序数组,如果第一个数小于最后一个数,说明没有旋转或者旋转了一轮回归原位了,如:112335。如果不是,最小的数只会出现在右侧的有序子数组中,从后往前遍历找到即可。注意:nums[tail] >= nums[tail-1],因为用重复,所以判断时有等号
class Solution { public: int findMin(vector<int>& nums) { if (nums.size() == 0) return -1; int tail = nums.size()-1; if (nums[0] < nums[tail]) return nums[0]; else { while (tail > 0 && nums[tail] >= nums[tail-1]) tail--; } return nums[tail]; } };这个代码好简洁我靠
class Solution {
public:
int findMin(vector[HTML_REMOVED]& nums) {
if(nums.size()==0)return -1;
sort(nums.begin(),nums.end());
return nums[0];
}
};
感觉题目要加强,把这种捷径断掉
但是查找的是最小值,这样方法是卡不掉的,除非数据量开到nlogn过不去,但是力扣的数据也不会那么强
class Solution {
public:
int findMin(vector[HTML_REMOVED]& nums) {
int n = nums.size();
if(n==0) return -1;
int i = 0;
while(i<n-1 && nums[i]<=nums[i+1]) i++;
if(i<n-1) return nums[i+1];
else return nums[0];
}
};
class Solution { public: int findMin(vector<int>& nums) { int len = nums.size(); if(len==0) return -1; while(nums[0]==nums[len - 1]) --len; int mid, l = 0, r = len - 1; if(nums[l]<nums[r]) return nums[l]; //这样写会比相对慢一点,希望这个思路对大家有帮助 while(l<r) { mid = l + r >> 1; //中间那个数比最右边的数大,说明现在这个mid在左边的递增区间,/* [3,4,6,7] [0,1,2] */ if(nums[mid]>nums[r]) l = mid + 1; else //中间那个数比最右边的数小,说明现在这个mid在右边的递增区间,/* [3,4] [0,1,2] */ { r = mid; } } return nums[l]; } };if (nums[n] >= nums[0]) return nums[0];这一行应该可以省掉吧
可以,当满足这个条件说明数组没有进行反转,直接进行二分也可以。但是有这个判断,代码会跟快。
我去掉这一行之后是错误答案
可以去掉hh
完全旋转的数组是一种特殊情况,所有去掉是错误的
或者你把这行代码改掉就可以了: while(n > 0 && nums[n] >= nums[0]) n –;
我傻了
int findMin(int* nums, int numsSize)
{
if (numsSize == 0) return -1;
if (numsSize == 1) return nums[0];
for (int i = 1; i <= numsSize; i++)
if (nums[i] < nums[i - 1]) return nums[i];
return nums[0];
}
这个题如果要二分的话,是不是也可以去前面重复的
*-
让相邻两个数相减,前面的数减去后面的数,只有在遇到最小的数的时候,相减结果才有可能>0,这样也可以诶!不过二分好高级!学到了!!!
class Solution { public: int findMin(vector<int>& nums) { int i=0; int n=nums.size(); //数组为空 if(n==0) return -1; for(i=0;i<n;i++) { if(nums[i]-nums[(i+1)%n]>0) return nums[(i+1)%n]; } //如果在循环里面一直没有找到,全部都是相减≤0,那么只有全部相等的情况 return nums[0]; } };这个就算直接遍历了 二分法时间小一点
没找到还有没旋转的时候
billkin真帅
二分的本质是某种性质的分界点,学到了,哈哈
感觉不用二分。。。。
class Solution {
public:
int findMin(vector[HTML_REMOVED]& nums) {
if(nums.empty()) return -1;
int t=nums[0];
for(auto c:nums)
{
if(c<t)
return c;
}
return t;
}
};
我当时也是这样想的
for(int i=0;i<nums.size();i++)
{
if(nums[i+1]<nums[i])return nums[i];可行?
}
最后应加一个return nums[0],因为旋转之后的数组可能与原数组相同
这样子最坏是O(N),卡复杂度好像就过不了了
请问,这个输入数据应该不是旋转数组吧[0, 1, 3, 5, 5, 5, 7, 8, 9, 9, 9, 9, 10, 11, 12, 14, 15, 16, 18, 18, 18, 22, 23, 23, 24, 25, 26, 27, 27, 27, 30, 31, 32, 33, 34, 34, 35, 36, 36, 37, 39, 39, 44, 45, 46, 46, 47, 48, 49, 49, 49, 54, 55, 56, 58, 58, 58, 59, 59, 60]
这个是完全旋转