逆序对的数量

思路分析

1. 暴力做法

每一个数向后面依次遍历，时间复杂度是$O(n^2)$,本题数据是$10^5$，$C++$一秒能算$10^7 ~ 10^8$，必然超时

2. 分治思想,利用归并排序

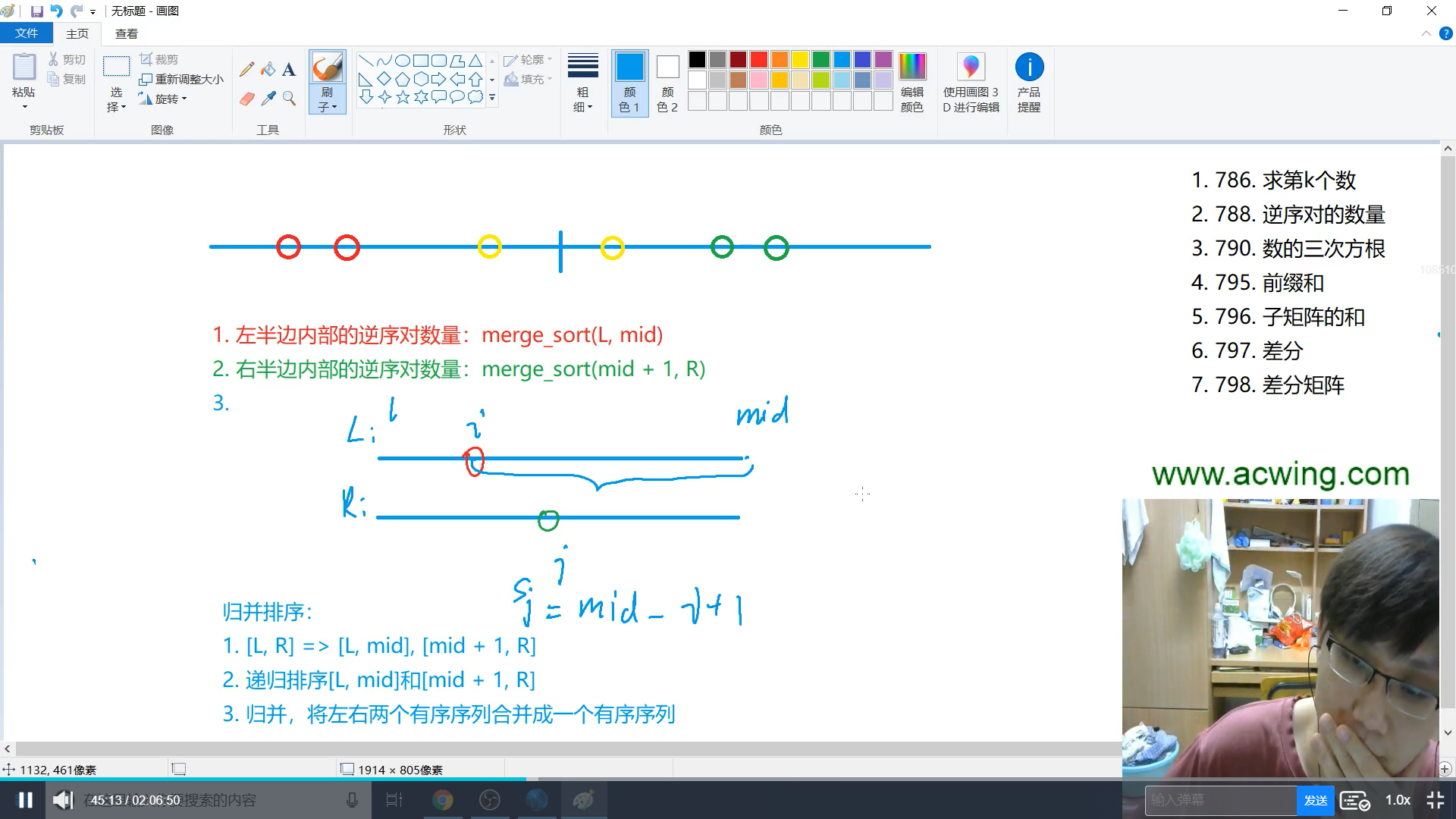
首先逆序对分为三种
1. 左半区间内
2. 右半区间内
3. 横跨两个区间
我们让归并排序能够返回该区间内的逆序队数量，那么前两种情况，我们可以通过递归实现
LL res = merge_sort(q, l, mid) + merge_sort(q, mid + 1, r);
横跨两个区间的逆序队，在归并时，当前半部分的某个数$a[i] > $后半部分某个数字$b[j]$时，对于后面的数字，前半部分里，$a[i]$以及它后面的数字都可以与$b[j]$构成逆序对
所以以$b[j]$为后面的数，构成逆序对的数量是$mid - l + 1$， 当前面或者后面有遍历完时，就不存在新增逆序对了，所有的再先前已经被计算过

数量级问题

本题会爆$int$，极限情况逆序，是$O(n^2)$级的逆序对数量，int类型最大是$2 * 10$^$10$，很可能爆int(实测会爆int)，所以答案用long long存储

时间复杂度

是归并基础上附加了额外信息，所以时间复杂度同归并$O(n\log n)$

代码

#include <iostream>

using namespace std;

typedef long long LL;

const int N = 1e5 + 10;

int a[N], tmp[N];//归并需要辅助数组

LL merge_sort(int q[], int l, int r)
{
    if (l >= r) return 0;//当区间内只有一个数时，不存在逆序对返回0

    int mid = l + r >> 1;

    LL res = merge_sort(q, l, mid) + merge_sort(q, mid + 1, r);//递归处理在单边的逆序对数量

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else
        {
            res += mid - i + 1;//计算以q[j]结尾的逆序对数量
            tmp[k ++ ] = q[j ++ ];
        }
    while (i <= mid) tmp[k ++ ] = q[i ++ ];//扫尾
    while (j <= r) tmp[k ++ ] = q[j ++ ];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];//归位

    return res;
}

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);

    cout << merge_sort(a, 0, n - 1) << endl;

    return 0;
}