第k个数

思路分析

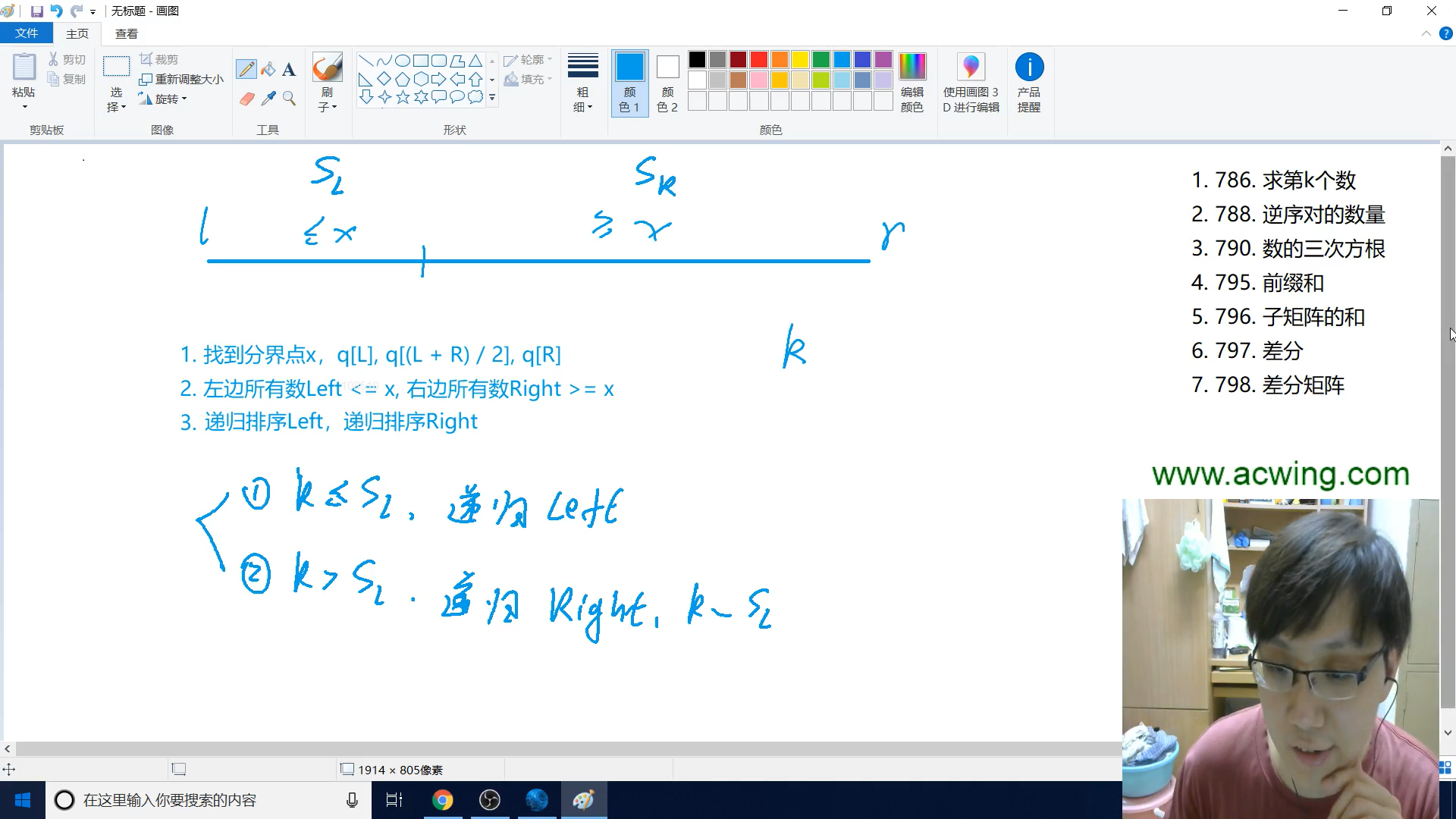
硬写的话，其实可以先排序再输出第$k$大的数，时间复杂度是$O(n\log n)$，但是快速选择可以以$O(n)$的时间复杂度做出来(证明在后面)

快排的一个缺点是，分左右边时候，左边所有数字 $ <= $右边，一个数只会在左边或是右边，那么快排左边和右边总有一个是无效的，那我们就可以通过判断第$ k $个数在左或是在右来减少冗余操作

快排结束分界点是$ j $，左部分，数字有j - l + 1个
所以当 k <= j - l + 1时，$k$ 是左边的第$k$大数，快排左边
否则第$k $个数在右边， 是右边第k - (j - l + 1)大数，所以递归处理右部分

递归截止条件: $l >= r$

时间复杂度分析

平均情况下，是每次选取原长度的一半进行递归，$ 1 + 1/2 + 1/4 + .... $，等比数列求和可知是$O(n)$的时间复杂度

代码

#include <iostream>

using namespace std;

const int N = 100010;

int q[N];

int quick_sort(int q[], int l, int r, int k)
{
    if (l >= r) return q[l];//递归截止

    int i = l - 1, j = r + 1, x = q[l + r >> 1];//快排模板
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }

    if (j - l + 1 >= k) return quick_sort(q, l, j, k);//k在哪边就递归处理哪边
    else return quick_sort(q, j + 1, r, k - (j - l + 1));
}

int main()
{
    int n, k;
    scanf("%d%d", &n, &k);

    for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);

    cout << quick_sort(q, 0, n - 1, k) << endl;

    return 0;
}