差分矩阵

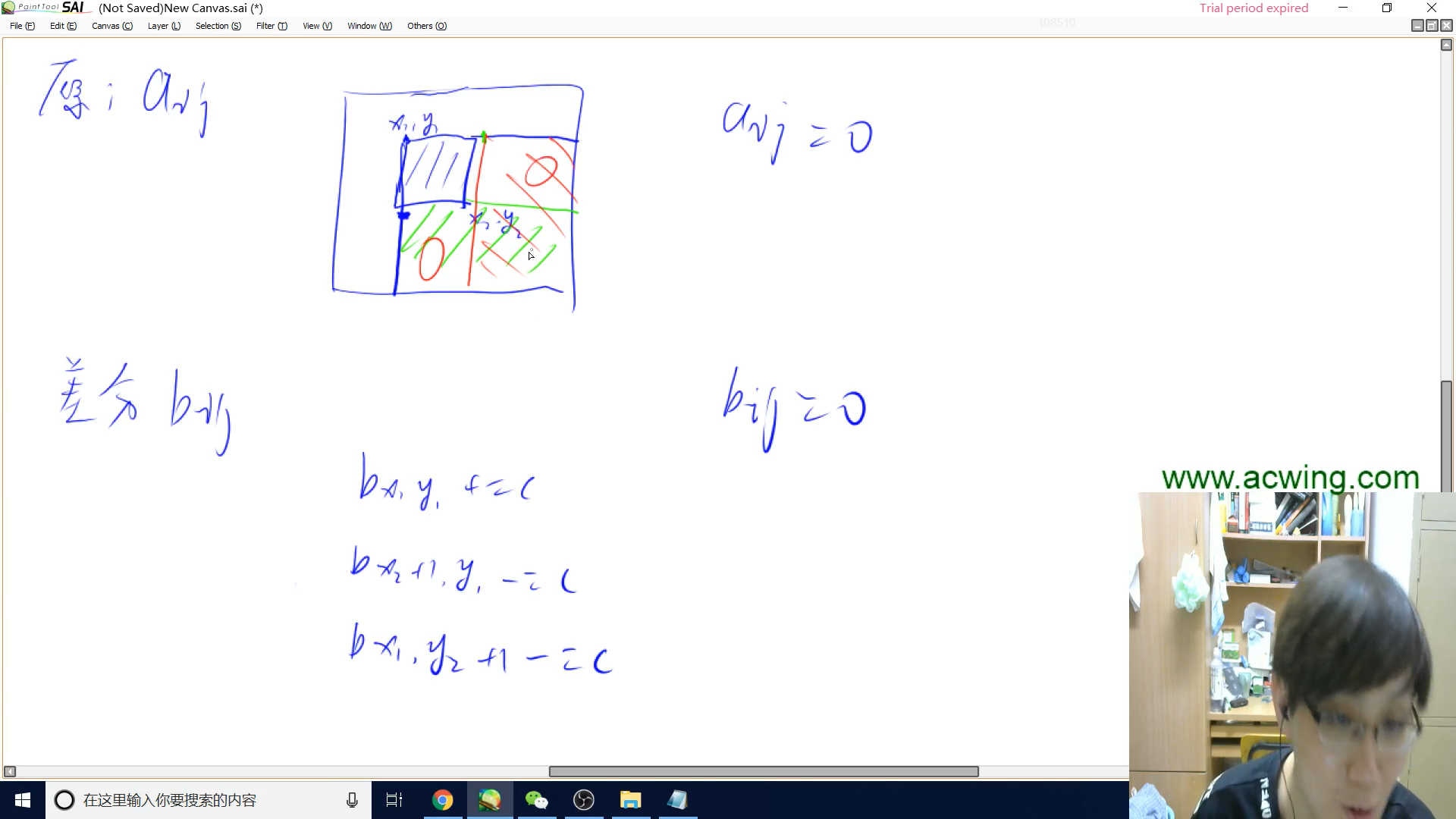
二维差分概述

$a[N][N]$是前缀和矩阵，$b[N][N]$是差分矩阵
前缀和与差分为互逆运算

二维差分的作用

当想给一个子矩阵加上一个同一个常数$c$，如果一个一个加，那么时间复杂度是$O(n)$的，($n$表示矩阵所有元素个数)，而用差分矩阵操作需要$O(1)$。如果这样操作数量较大时，差分矩阵的时间优势就会很大了

差分操作

见上图与模板，改变差分矩阵的四个元素就可以改变前缀和子矩阵的所有元素(空间想象二维数组即可)

二维差分的初始化

1. 利用前缀和定义，移项可得， $b[i][j] = a[i][j] + a[i - 1][j - 1] - a[i - 1][j] - a[i][j - 1];$
2. 把前缀和矩阵看成，从全$0$矩阵每一个元素依次执行插入操作(y总的选择)

二维差分模板

// 给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c

代码

#include <iostream>

using namespace std;

const int N = 1010;

int n, m, q;
int a[N][N], b[N][N];//a[N][N]是前缀和矩阵, b[N][N]是差分矩阵

void insert(int x1, int y1, int x2, int y2, int c)//差分操作
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main()
{
    scanf("%d%d%d", &n, &m, &q);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &a[i][j]);//读入前缀和矩阵

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            insert(i, j, i, j, a[i][j]);//初始化差分矩阵

    while (q -- )
    {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);//差分操作
    }

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];//y总习惯在差分矩阵上求出前缀和矩阵

    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 1; j <= m; j ++ ) printf("%d ", b[i][j]);
        puts("");
    }

    return 0;
}