子矩阵的和

二维前缀和概述

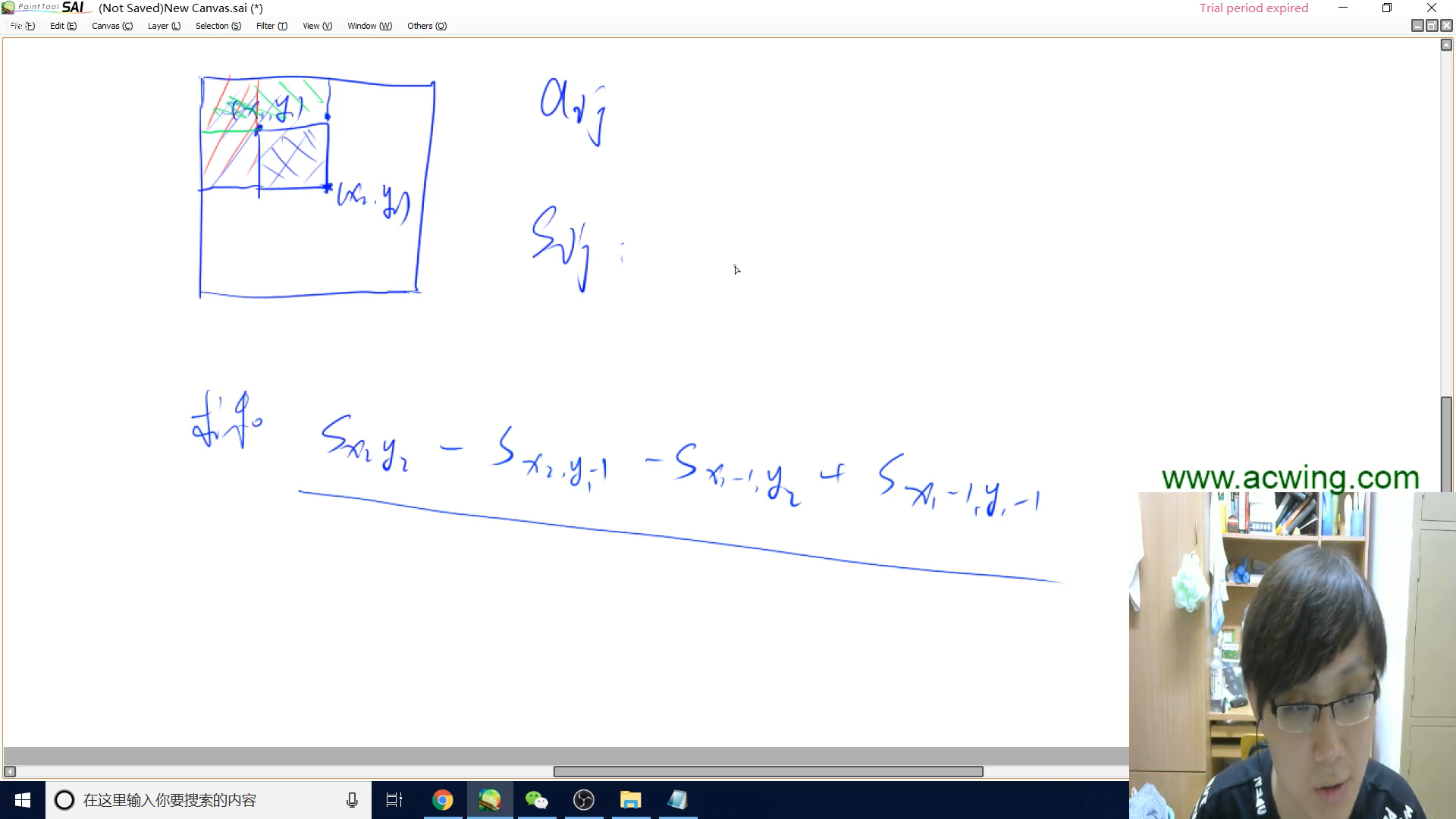
二维前缀和是为了快速求出子矩阵内所有元素的和

要把二维前缀合想象成矩阵(二维数组)的划分，y总上课正方形划分，当时第一次上，我老认为坐标是一个点，但其实坐标是一个数字

Y总里面，$x$表示是行， $y$表示列，后面偏移量表示$x, y$意思还是这个

$x2, y2$表示二维数组的一个元素， $a[N][N]$表示原数组， $s[N][N]$是前缀和数组
$s[x2][y2]$表示从左上角$(0, 0)$到右下角$(x2, y2)$的矩形内所有元素的和

前缀和的核心是公式

计算前缀和 $:$
$s[x2][y2] = s[x2 - 1][y2] + s[x2][y2 - 1] + a[x2][y2] - s[x2 - 1][y2 - 1]$
求子矩阵和 $:$
以$(x1, y1)$为左上角，$(x2, y2)$为右下角
子矩阵和为 $s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y2 - 1]$

思路分析

y总非常巧妙的开了一个数组，先作为原数组，后来再作为二维前缀和数组
因为前缀和数组每次都是别的前缀和$+$右下角点元素之和
而且，别的前缀和是在本前缀和之前计算完，所以可以少开一个数组，在原数组上计算前缀和而后输出

代码模板

二维前缀和
S[i, j] = 第i行j列格子左上部分所有元素的和

以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

代码

#include <iostream>

using namespace std;

const int N = 1010;

int n, m, q;
int s[N][N];//原矩阵兼前缀和矩阵

int main()
{
    scanf("%d%d%d", &n, &m, &q);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &s[i][j]);//输入原矩阵

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];//求前缀和矩阵

    while (q -- )
    {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
        //求子矩阵的和
    }

    return 0;
}