前缀和

一维前缀和概述

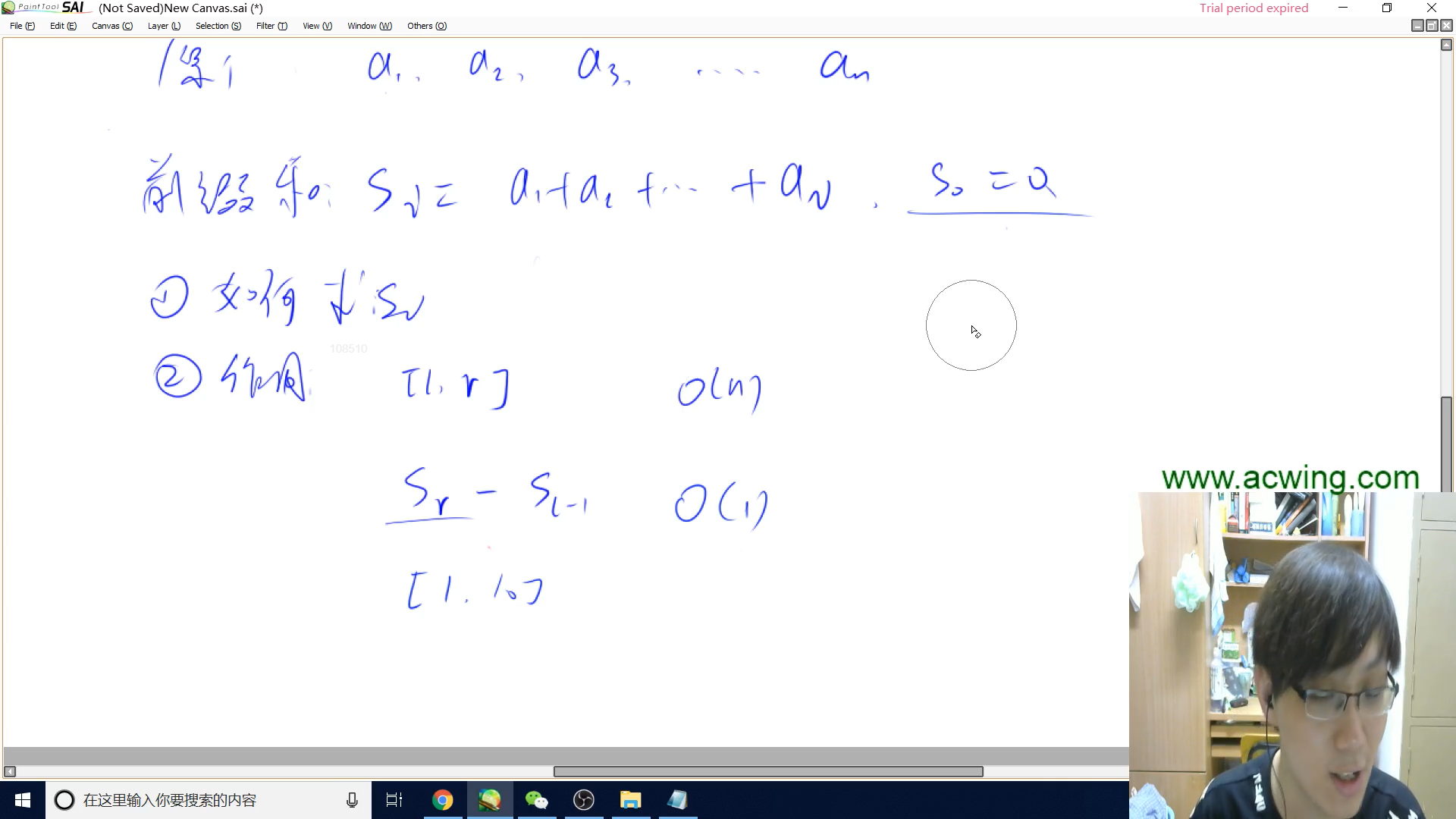
前缀和作用

前缀和是一种思想，可以在多次求区间和的时候用$O(1)$的时间求出来
如果不采用前缀和数组，是$O(N)$。前缀和数组需要额外开等大数组，以空间换时间

前缀和定义$:$

$a[N]$是原数组， $b[N]$是前缀和数组
$b[i] = a[1] + a[2] + .... + a[i]$
前缀和数组的下标是从$1$开始的

前缀和核心公式

前缀和的初始化$:$ $s[i] = s[i - 1] + a[i]$
求$a[l]$到$a[r]$的和$:$ $s[r] - s[l - 1]$

输入处理

数据规模大于一百万时，建议使用scanf

时空复杂度分析

时间$:$ 前缀和初始化$O(N)$, 每次查询$O(1)$，所以是O(n)
空间$:$ 开了一个辅助数组

前缀和代码模板

一维前缀和
S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]

代码

#include <iostream>

using namespace std;

const int N = 100010;

int n, m;
int a[N], s[N];

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);

    for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + a[i]; // 前缀和的初始化

    while (m -- )
    {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n", s[r] - s[l - 1]); // 区间和的计算
    }

    return 0;
}