高精度乘法

思路分析

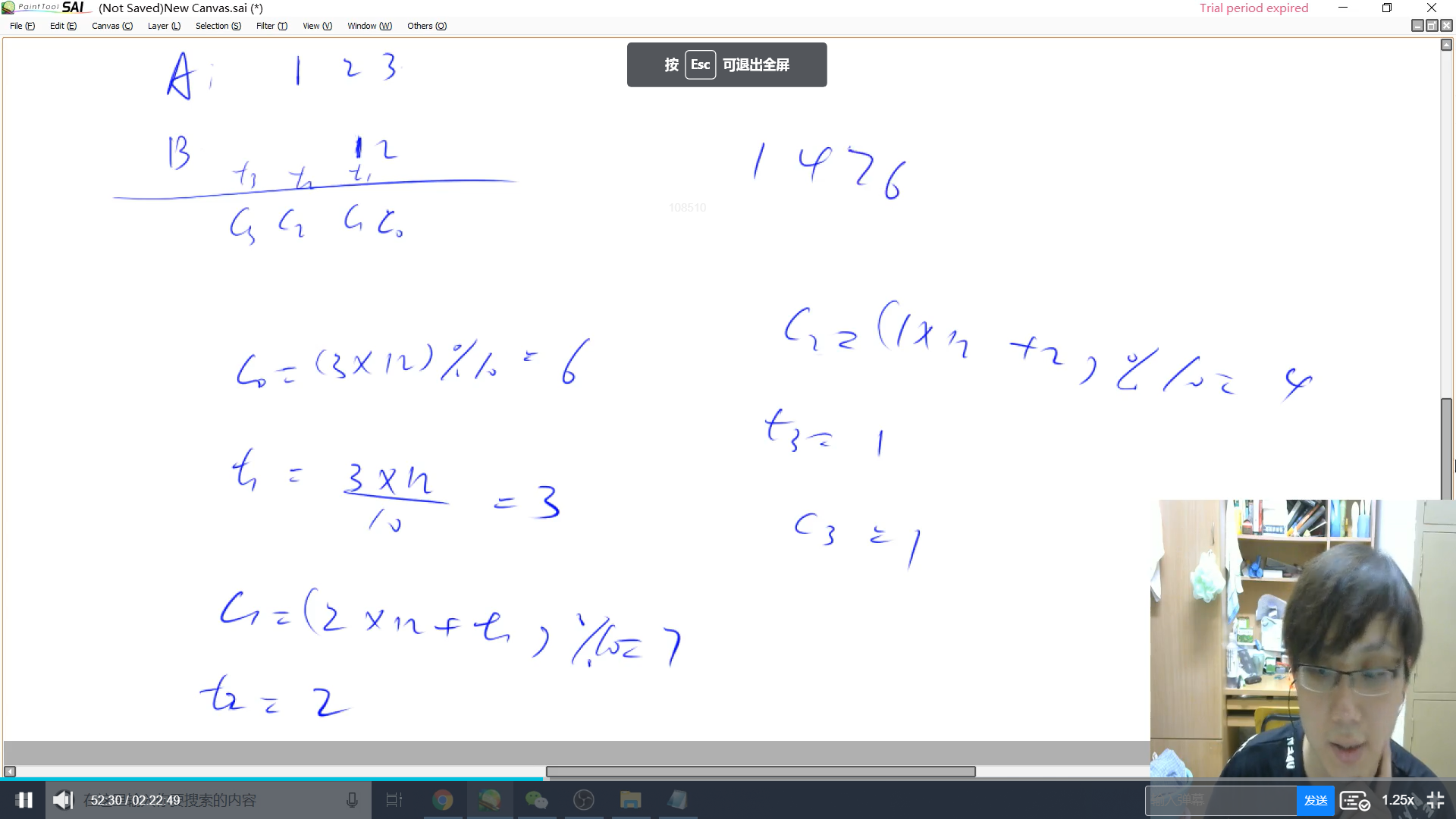
题目是一个大整数 * 小整数
这里面的表示和思路和前面一样，用$vector$倒叙存储

这里整体还是模拟手工运算，不过不是一位乘一位， 是分解成一位乘多位

$eg: 345 * 12 = 5 * 12 + 40 * 12 + 300 * 12$
$b$是小整数，所以可以乘

$t$表示每次运算剩下来需要进位的数(这里建议手工模拟一下算法流程)

代码

#include <iostream>
#include <vector>

using namespace std;


vector<int> mul(vector<int> &A, int b)
{
    vector<int> C;

    int t = 0;//进位，这里进位是由大整数的某一位乘小整数出来的，所以t的值可以大于10
    for (int i = 0; i < A.size() || t; i ++ )//当A还有位数要拿去乘，或者t进位还存在
    {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);//放入答案
        t /= 10;//答案除以权重10，转换到下一位
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();//去除前导0

    return C;
}


int main()
{
    string a;
    int b;

    cin >> a >> b;

    vector<int> A;
    for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');

    auto C = mul(A, b);

    for (int i = C.size() - 1; i >= 0; i -- ) printf("%d", C[i]);

    return 0;
}