高精度加法

高精度问题概述

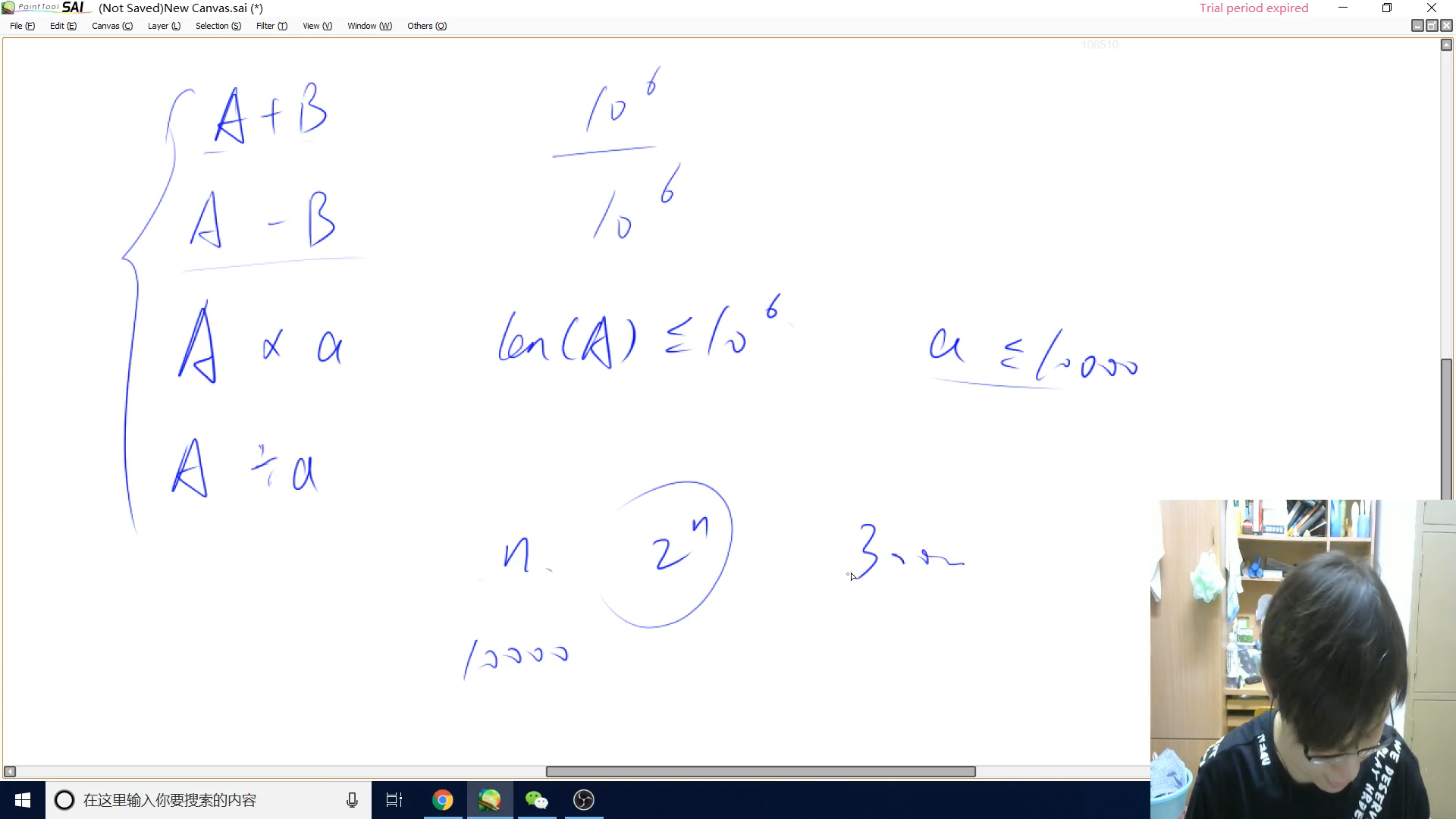
$C++$ 中没有大整数类，所以自己要写一下
常见的有四类：
前提条件，下面的数字均大于0

1. 大整数A + 大整数B

2. 大整数A - 大整数B

3. 大整数A * 小整数B

4. 大整数A / 小整数B， 求商和余数

高精度加法概述

高精度计算的主要思想都是模拟人手工计算

1. 数据存储:

$(1)$ 我们需要知道数的位数，采用$vector$(动态数组)去存储

$(2)$ 其次，为了方便，我们需要倒序存储，即数组最高位存个位(最低位)。原因是进位时，若是正序存储，我们需要移动整个数组，效率低下

$(3)$ 高精度计算穿插出现在一个题，所以我们的四个高精度题的存储是一样的

2. 本题目的思路:

$(1)$ 首先是数据读入，由于数字位数很大，采用字符串进行读入，然后将它挨个字符扣到$vector$里面

$(2)$ 核心部分, $t$表示进位，初始化为$0$。每次加法时，如果A存在加上A的该位，B该位存在就加B的该位

$(3)$ $C$用来存答案，每次放进去的是$t % 10$，下一次进位是 $t / 10$

$(4)$ 加法执行完后，如果进位还存在就把它存到$vector$里面

$tips:$ 这里建议如果代码硬读不通的，按该流程手工模拟几次就可以知道每一句话的意思了

代码

#include <iostream>
#include <vector>

using namespace std;

vector<int> add(vector<int> &A, vector<int> &B)
{
    if (A.size() < B.size()) return add(B, A);
    //确保A 位数大于 B， 方便后面写代码

    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i ++ )
    {
        t += A[i];
        if (i < B.size()) t += B[i];
        //由前面得，A位数大于等于B位数，所以B存在就加上B，A加的时候没有判断
        C.push_back(t % 10);//计算本位答案
        t /= 10;//求出下一位进位
    }

    if (t) C.push_back(t);//如果进位还在，就放入答案
    return C;
}

int main()
{
    string a, b;
    vector<int> A, B;
    cin >> a >> b;
    for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');
    //将数据从字符串读入向量，数组第一位存个位，依次类推
    for (int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');

    auto C = add(A, B);
    //auto c++ 11 关键字，自动类型推导
    for (int i = C.size() - 1; i >= 0; i -- ) cout << C[i];
    cout << endl;

    return 0;
}