题目描述

n-皇后问题是指将 n 个皇后放在 n∗n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

现在给定整数n，请你输出所有的满足条件的棋子摆法。

输入格式

共一行，包含整数n。

输出格式

每个解决方案占n行，每行输出一个长度为n的字符串，用来表示完整的棋盘状态。

其中”.”表示某一个位置的方格状态为空，”Q”表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

数据范围

1≤n≤9

样例

输入样例：
4
输出样例：
.Q..
...Q
Q...
..Q.

..Q.
Q...
...Q
.Q..

题目分析: (范围较小时优先考虑大爆搜)
众所周知,这是一道经典的 DFS  回溯问题：回溯:当前状态如果不行,就再回到上一个状态,直到返回到最初,注意回到上一个状态的时候
需要 ‘还原现场’,这点很重要.
通过题中的样例我们可以发现,每一行只能有一个 皇后,当一行有一个皇后后,我们就能去判断接下来的
行中是否可以放一个 皇后 ,如果说这一行的位置都判断完了还是没有办法放一个皇后,说明上一个状态
不足以达到正确的答案,这个时候我们就需要回溯到上一个状态进行再次递归。
重点看下图:（图片来源网络）

如果上面的图没有看懂,我推荐一下这个大佬的博客,关于这个问题展示的非常清晰:

https://blog.csdn.net/zhang245754954/article/details/52612784

这道问题我重点想说一下关于怎么判断斜侧方是否可以放一个皇后,当然会的小伙伴就可以略过了,不过既然来
了不妨看一看,如解释的不到位,还烦请各位指出为题,在下非常感谢.
好了,重点来了:
先看下面这张图(自己画的,可能不是十分到位,将就看一下吧)删除线不会弄，hhhhhhh

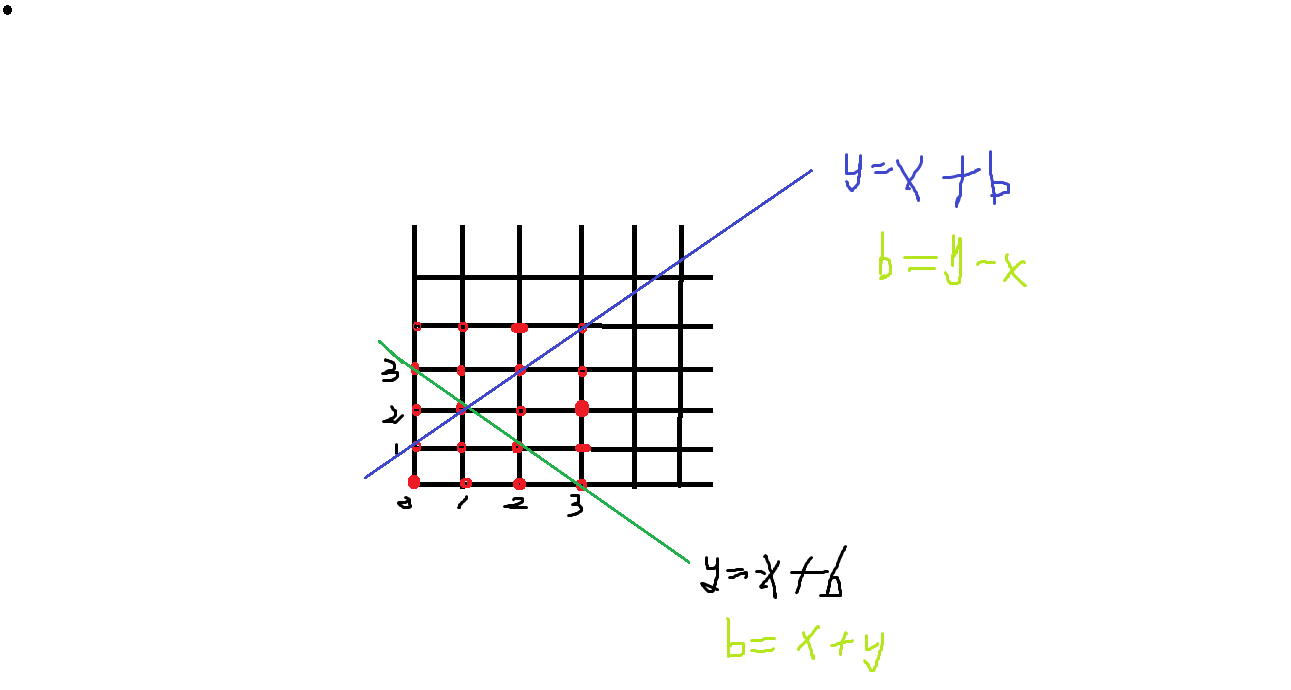
看图可以知道:有两条斜线 : y = x + b, y = -x + b(因为是正方形,所以斜率分别为 -1 和 1)
转换一下可以得出        : b = y - x, b = y  + x;
也就是说 : 在 y = -x + b 这条线上,我们得到的两个点横纵坐标相加 相等。
举例来说 ：点(1,2)和点(0,3)同在 y = -x + b 这条直线上,横纵坐标相加是不是相等,就是这么神奇
           另一条直线同理,这就为我们下面判断斜侧方是否有皇后奠定了坚实的基础。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<cstdio>
#include<string.h>
#include<limits.h>
#include<vector>
#include<deque>
#include<queue>
using namespace std;
const int maxn = 20;                   // 这里需要开到 2 倍的空间,防止越界
char graph[maxn][maxn];
bool col[maxn],dg[maxn],udg[maxn];     // col:标记列,dg: 正对角线, udg: 反对角线
int n;
int main(void) {
    void DFS(int u);
    scanf("%d",&n);
    for(int i = 1; i <= n; i ++) {     // 初始化
        for(int j = 1; j <= n; j ++) {
            graph[i][j] = '.';
        }
    }
    DFS(1);
    return 0;
}
void DFS(int u) {                      //  u 代表行(我们逐行判断)
    if(u == n + 1) {                   //  当到最后一行时,说明该方案可行,输出即可
        for(int i = 1; i <= n; i ++) {
            for(int j = 1; j <= n; j ++){
                cout<<graph[i][j];
            }
            cout<<endl;
        }
        cout<<endl;
        return ;
    }
    for(int i = 1; i <= n; i ++) {      // i 代表第几列,我们需要判断每行的每个元素是否可以放这个皇后
        if(!col[i] && !dg[u + i] && !udg[n - u + i]) { 
        // 根据上述图的解释我们可以得到上述判断,[u + i]代表反对角线(i = -u + b),后面的代表正对角线
        // 后面的为啥要 + n 呢？为了防止出现负数，然后越界的情况,因为 后面的方程是 i = u + b
        // b = i - u ,当 u 比 i 大时就会出现负数(数组没有负数下标)(所以都 + n)同样的数组空间应该开 2 倍
            col[i] = dg[u + i] = udg[n - u + i] = true; 
            graph[u][i] = 'Q';
            DFS(u + 1);
            col[i] = dg[u + i] = udg[n - u + i] = false;
            graph[u][i] = '.';
        }
    }
    return ;
}