数的范围

二分概述

这道题是标准的二分问题。
首先，二分的本质是一个区间划分问题，它的左边满足一种性质，右边满足另一种性质。那么我们就可以通过二分法，求出这两个性质的边界(根据需求可以求出满足左侧还是右侧性质的边界)
如果一个区间具有单调性，那么一定可以二分。没有单调性，也可能可以二分，单调性是一个充分条件。
二分问题分为整数二分和浮点数二分两种。整数二分存在边界问题，比较难。浮点数则较为简单。

整数二分模板

有两个模板，根据情况筛选用哪一个

bool check(int x) {/* ... */} // 检查x是否满足某种性质, 这是依据题目实现的一个具体逻辑

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}

// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

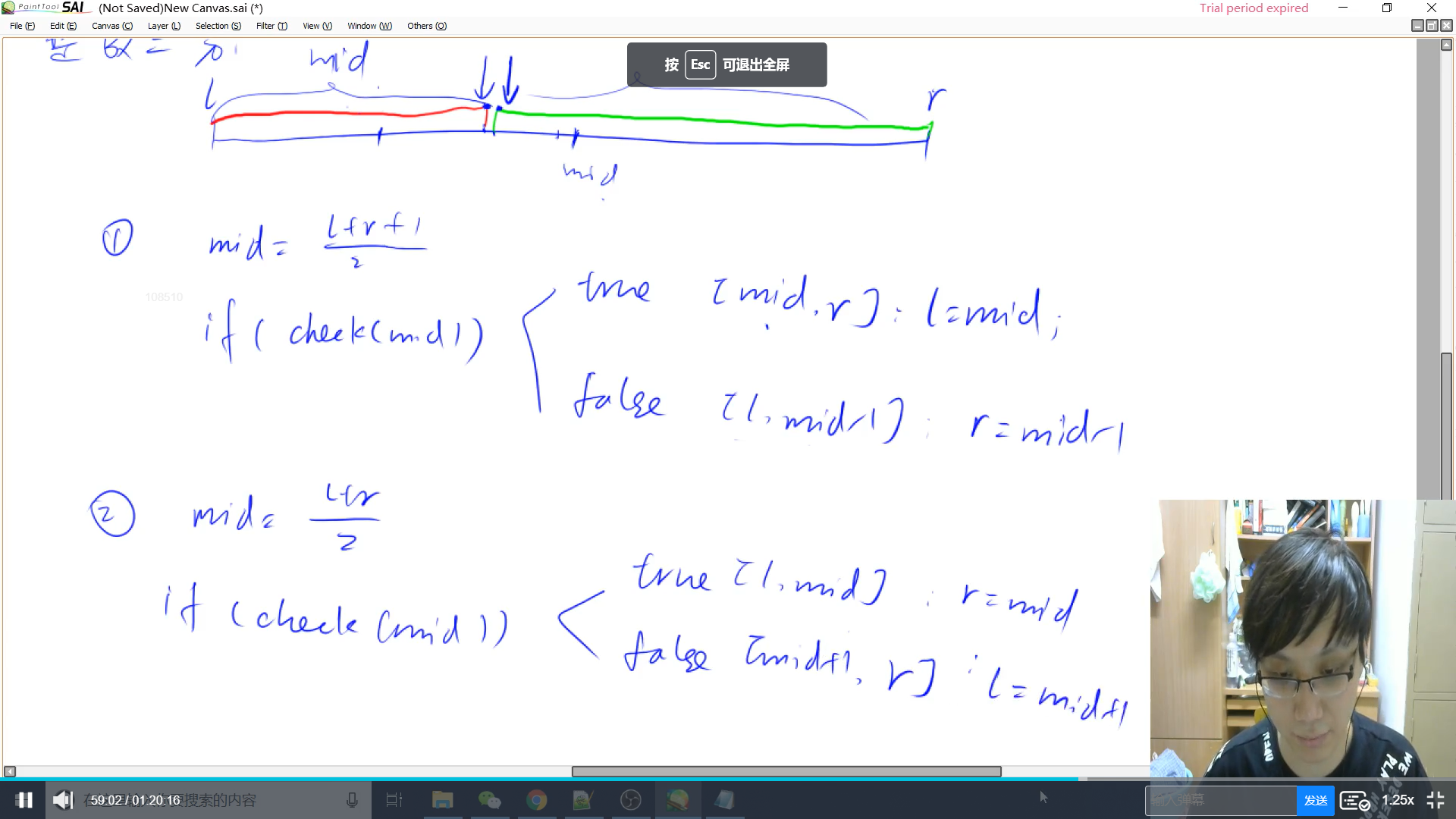
红绿是代表着两种不同性质，我们二分出来的结果便是红绿边界(根据需求，可以是红色右边界，或者绿色左边界)

我们首先检查中点(可以向上或者向下取整)是否满足性质，满足性质后，根据需要二分出的边界判断下一步二分的区间范围，(就是$r = mid$, 还是$l = mid$)。

这时候如果$l = mid$, 那么中点需要向上取整(即$l + r + 1 >> 2$)，如果不这样会出现死循环(参考上课内容)，$r = mid$则选择向下取整($mid = l + r >> 1$)

更新后，就会不断二分，直到答案出现

本题目的思路分析

题目输入是单调序列，所以肯定可以采用二分法
我们寻找起始位置时候，可以考虑一个性质，$>=$ 输入元素，那么二分出从左向右向右的第一个点(该性质边界)即可
寻求结束位置时，另一个性质 $<=$ 输入元素，那么二分出从右向左第一个满足该性质的第一个点(边界)即可

tips

二分结束时候, $l == r$, 所以返回$l$或者$r$都可以

时间复杂度

每次都将范围缩小一半，最终范围内只有一个数字时候停下来
所以是$O(\log n)$

数据规模，$1e5$, 一万组询问
$1e4 * log(1e5) = 16w$， 可以求出

代码

#include <iostream>

using namespace std;

const int N = 100010;

int n, m;
int q[N];

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);

    while (m -- )
    {
        int x;
        scanf("%d", &x);
        //求起始端点
        int l = 0, r = n - 1;//二分区间，0 ~ n - 1
        while (l < r)
        {
            int mid = l + r >> 1;
            if (q[mid] >= x) r = mid;// r = mid, mid向下取整
            else l = mid + 1;
        }

        if (q[l] != x) cout << "-1 -1" << endl;
        //我们找出来的是第一个 >= x的数，如果这个数不等于x，说明数组里没有这个数
        else
        {
            cout << l << ' ';
            //二分出终止端点
            int l = 0, r = n - 1;
            while (l < r)
            {
                int mid = l + r + 1 >> 1;
                if (q[mid] <= x) l = mid;// l = mid, mid 记得 + 1，向上取证 
                else r = mid - 1;
            }

            cout << l << endl;
        }
    }

    return 0;
}