归并排序

归并排序概述

归并排序也是一种分治算法。和快排不同的是，归并排序是先递归处理，而快排是后递归处理。归并需要辅助空间，而快排不需要。

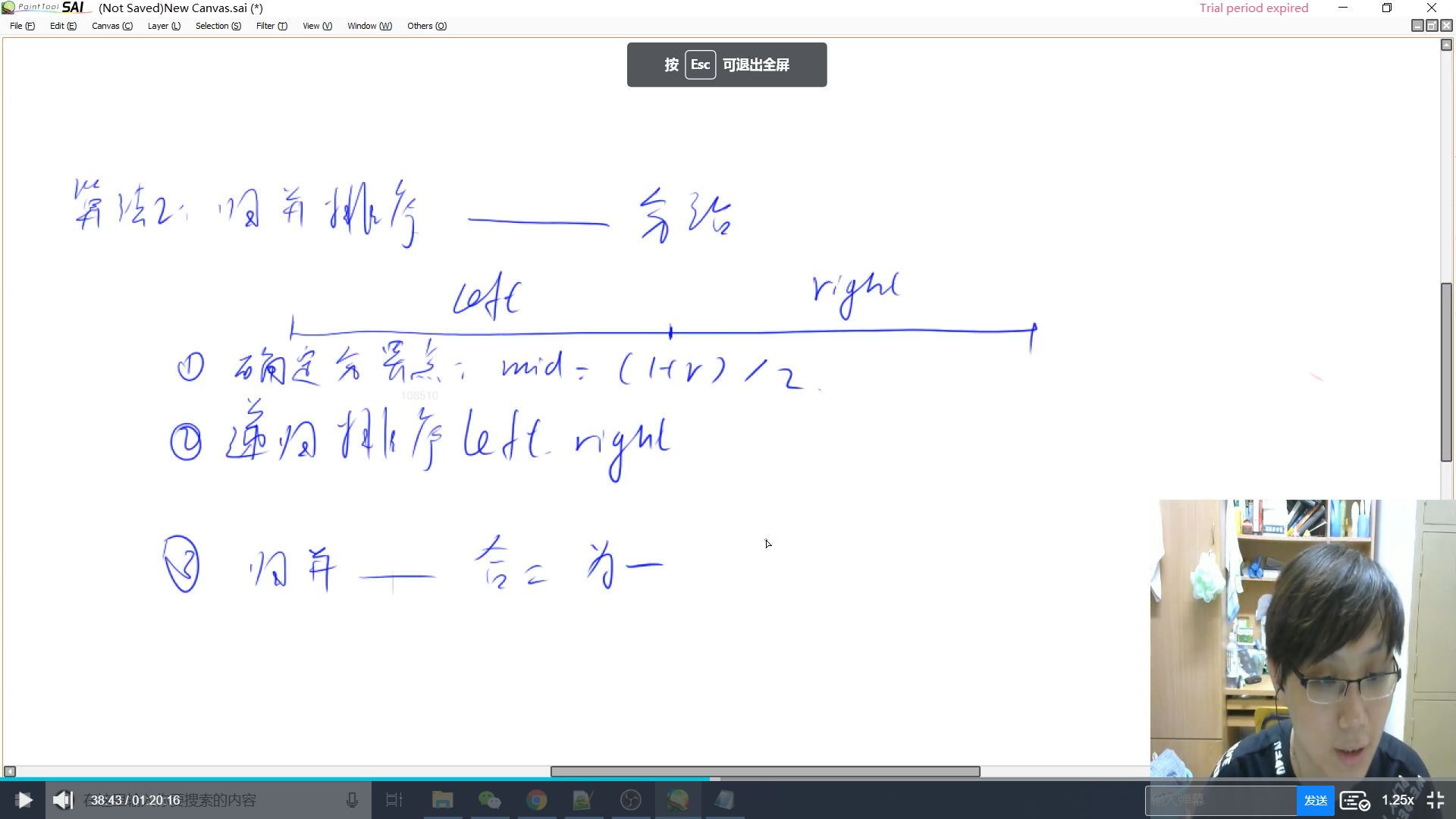
算法思路

$1.$ 确定分界点也就是中点, int mid = l + r >> 1

$2.$ 递归处理左右两部分归并排序的最终效果是让区间内的数组有序，所以递归左右后得到的左右部分也都是递增有序的

$3.$ 归并–合二为一。这也是一个双指针算法，对于两个序列，它维护了大小次序。每次选择小的放入临时数组(一样大时，将第一个数组的放进去，维持稳定性)。当一个数组完了，而另一个还有的时候，将另一个依次放入tmp数组。最后，将tmp数组的内容拷贝回原数组的对应区间，这时，这一个区间就是归并后有序递增的了。 递归结束条件是区间内没有或仅有一个数字

常见问题

初学可能会对递归左半部与右半部有些疑问，这里引用数据结构与算法分析对递归的一些介绍

递归的四条基本法则

1. 基准情形

必须有某些基准的情形。它们不需要递归就能求解

2. 不断推进

对于那些需要递归求解的情形。递归调用必须能够向着产生基准情形的方向推进

3. 设计法则

假设所有的递归调用都可以正常运行

4. 合成效益法则

在求解同一问题的同一实例时，切勿在不同的递归调用中做重复性工作

对于递归调用，我们不需要知道它的具体实现细节(手工模拟几次递归调用就能有些感觉)，它满足上述条件，便可以求出来应有的答案

时间复杂度

因为每次都是严格的分成两部分，所以是严格的$O(n\log n)$
数据规模$1e6$,同快排可以求解出来

代码

#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int a[N], tmp[N];//tmp即辅助数组

void merge_sort(int q[], int l, int r)
{
    if (l >= r) return; // 递归结束条件， l >= r

    int mid = l + r >> 1;

    merge_sort(q, l, mid), merge_sort(q, mid + 1, r);//递归处理左半部分与右半部分

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)//合并开始，双指针算法
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else tmp[k ++ ] = q[j ++ ];
    while (i <= mid) tmp[k ++ ] = q[i ++ ];//如果第一个序列还有剩余的，就统一加过去
    while (j <= r) tmp[k ++ ] = q[j ++ ];
    //如果第二个还有余留。当然这一行与上一行最多只有一个会执行下去

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];//从辅助数组中拷贝回来有序的元素
}

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);

    merge_sort(a, 0, n - 1);//左右边界是0, n - 1

    for (int i = 0; i < n; i ++ ) printf("%d ", a[i]);

    return 0;
}