算法提高课汇总

算法思路

LCIS : LCS与LIS的结合, Y氏DP分析 :

状态表示 dp[i][j]

• 集合 : 首先考虑对于一个序列的LIS的集合定义 : 以第$i$个元素为结尾的所有上升子序列. 按此思路我们
  每次固定$b_j$作为上升子序列的结尾 : dp[i][j]表示由$a[1\sim i]$和$b[1\sim j]$元素构成, 以$b_j$作为结尾
  的公共上升子序列.

• 属性 : Max

状态计算

以序列集合中是否包含$a_i$作为划分依据(集合固定存在$b_j$, 这种划分方式类似于LCS); 对于包含$a_i$的
子集, 再以序列的上一个(倒数第二个)元素(在b[]中查询)作为划分依据(类似于LIS的划分方式).

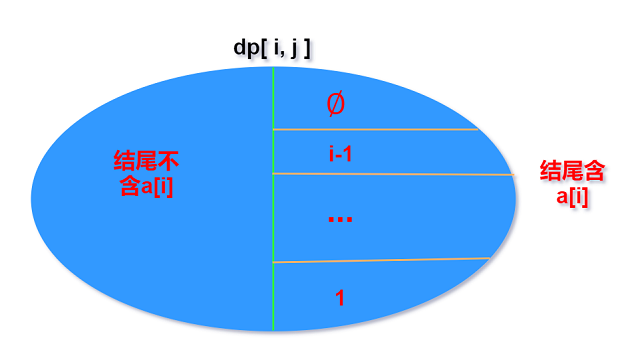
也就是对所有的公共上升子序列(所有集合)用$b_j$划分; 每个$b_j$对应子集再以是否含$a_i$作为划分.
因为我们固定了$b_j$而$a$属于一个范围, 所以问题可以变为对a[]判断是否公共, 对b[]计算上升.

从定义出发 :

• 对于序列不含$a_i$的部分: 对应集合变为由$a[1\sim i-1]$和$b[1\sim j]$元素构成, 以$b_j$作为结尾
  的公共上升子序列. 根据定义其对应最大值为$dp[i-1][j]$.

• 包含$a_i$的部分: 以上一个元素作为划分, 集合固定部分为末尾的($a_i = b_j$), 可变部分为
  $a[1\sim i-1]和b_k(b_k\lt b_j)$, 根据定义可变部分对应状态$dp[i-1][k]$.

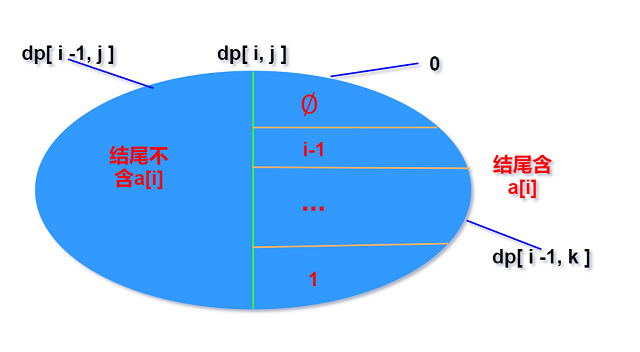
(这里我认为空集的权重是0而不是1, 1是$a_i = b_j$作为序列末尾的长度)

代码实现

$O(n^3)$版本

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 3010;

int n;
int a[N], b[N];
int dp[N][N];

int main()
{
    cin >> n;
    for( int i = 1; i <= n; i ++ )  cin >> a[i];
    for( int i = 1; i <= n; i ++ )  cin >> b[i];

    for( int i = 1; i <= n; i ++ )
    {
        for( int j = 1; j <= n; j ++ )
        {
            if( a[i] != b[j] )  
            {
                dp[i][j] = dp[i - 1][j]; //序列不含a[i]
                continue;
            }
            dp[i][j] = max( 1, dp[i - 1][j] ); //序列a[i]/b[j]的长度为1 
            //遍历上一个元素
            for( int k = 1; k < j; k ++ )
                if( b[k] < b[j] )
                {
                    dp[i][j] = max( dp[i][j], dp[i - 1][k] + 1 );
                }
        }
    }

    int res = 0;
    for( int i = 1; i <= n; i ++ )  res = max( res, dp[n][i] ); //以b[i]划分所有集合 所以遍历所有子集
    cout << res << endl;

    return 0;
}

$O(n^2)$版本

优化版本 : 代码的等价变形.

在对”上一个”元素遍历时, 其更新条件由于$a_i = b_j$可以更改为$b[k]\lt a[i]$, 此时最内存循环和$j$变量
无关, 每次我们用$dp[i-1][1\sim j-1]$中最大值更新. 我们可以用一个变量保存这个最大值, 并且在满足$b[j]\lt a[i]$时更新这个最大值.

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 3010;

int n;
int a[N], b[N];
int dp[N][N];

int main()
{
    cin >> n;
    for( int i = 1; i <= n; i ++ )  cin >> a[i];
    for( int i = 1; i <= n; i ++ )  cin >> b[i];

    for( int i = 1; i <= n; i ++ )
    {
        int maxv = 0; //保存前缀的最大值
        for( int j = 1; j <= n; j ++ )
        {
            if( a[i] != b[j] )  
            {
                dp[i][j] = dp[i - 1][j]; //序列不含a[i]
            }
            else
            {
                dp[i][j] = max( dp[i - 1][j], maxv + 1 ); //由a[i]存在与否划分的两个集合中的最大值
            }
            if( b[j] < a[i] )   maxv = max( maxv, dp[i - 1][j] ); //为下一个循环作准备
        }
    }

    int res = 0;
    for( int i = 1; i <= n; i ++ )  res = max( res, dp[n][i] ); //以b[i]划分所有集合 所以遍历所有子集
    cout << res << endl;

    return 0;
}