算法提高课汇总

算法思路

以输入为例, 一种最优的拦截方式 :

简单观察可知第一问求的是LIS(从右向左, 不严格), 可以用AcWing895.最长上升子序列相同的方法解决.

对于第二问, 考虑从左向右依次判断该导弹是否需要一个新的拦截系统拦截, 目标是需要的拦截系统最小.
对于每个拦截系统对应一个高度递减的数字序列, 我们只需要关注其最后一个导弹的高度即可, 这里用h
符号标记. 考虑一种贪心思路 :

• 在已有的拦截系统中, 将该导弹交给满足h大于它的系统集合中h最小的拦截系统拦截它.

• 若不存在上述拦截系统, 则需要一个新的拦截系统.

下面证明这个贪心思路的正确性.

两个证明策略

1. 证明两个数相等 : $a = b$ <--> $a\ge b \&\& b\ge a$.

2. 证明一个策略方案数不大于另一个方案数 : 调整法.

证明 :

我们用$A$表示贪心算法得到的序列(拦截系统)个数, $B$表示最优解的序列个数. 证明$A = B$ :

• $B\le A$ : 最优解表明$B$是所有拦截方案中系统数目最小的数值, 所以必定有$B\le A$.

• $A\le B$ : (调整法).

$\;\;$Y总的解释 : 假设贪心算法和最优解的拦截方案不同, 首先关注第1个不同点 :

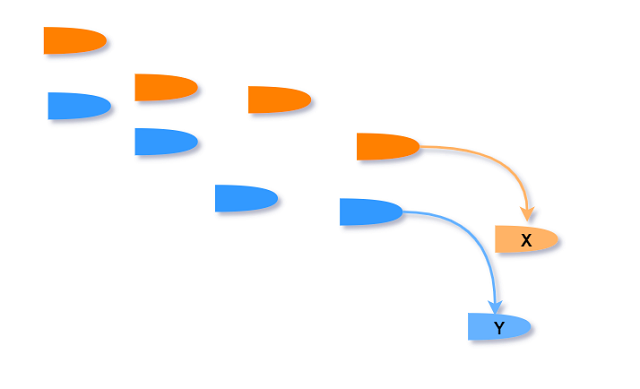
根据贪心思路导弹X应该选择蓝色系统, 而最优解X选择了橘色系统, 我们可以证明X和Y可以交换,
且交换后拦截系统的数量没有增加, 之后的不同也可用相同方法调整. 但这有一个令我困惑的地方 :
两个算法的拦截选择不是同时存在的. 所以稍加修改 :

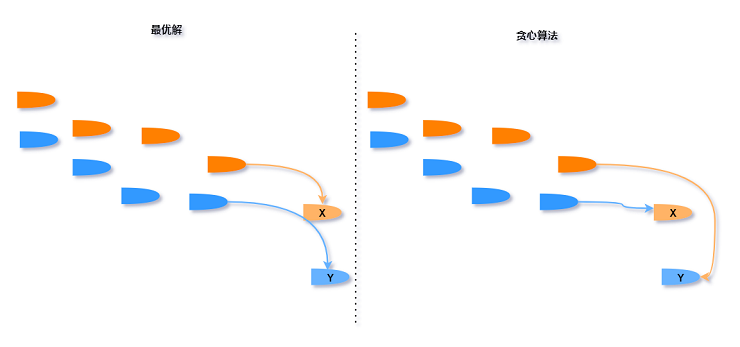
但这样理解贪心算法也有个问题, 两个算法第一个不同点并不一定是要X和Y的对称导弹. 所以这里
我按照从左向右依次选择导弹的过程中证明贪心算法的系统个数不大于最优方案 :

假设贪心算法和最优解的拦截方案不同, 第一个不同点在对导弹X的拦截方案 :

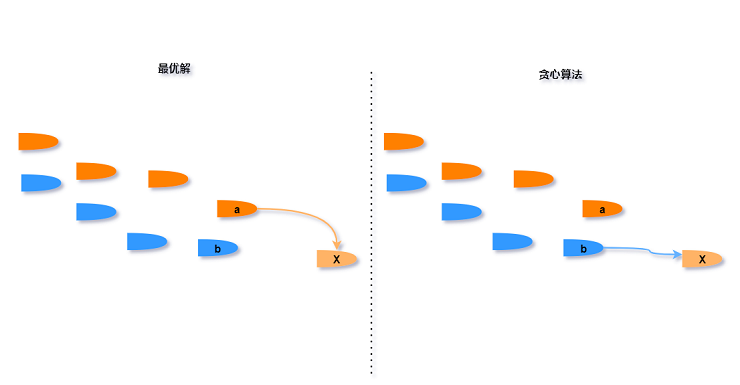
因为贪心策略是每次选择在满足拦截的条件下结尾导弹高度最低的, 所以在最优方案中对X的拦截可以调整为
与贪心方案相同, 此时我们只关注这两个拦截系统 : 原最优方案的结尾导弹高度为{b,X}, 调整后变为
{a,X}, $a\gt b$, 所以对于后续导弹的选择仍可以按照原本最优方案的选择.

同理可对后续的不同选择进行调整, 且这个过程中拦截系统数目不增, 所以可证得$A\le B$.

观察我们的贪心思路: 以结尾数值代表一个拦截系统, 并且每次对导弹$a_i$判断现有拦截系统中搜索满足
$f_j\lt a_i$的最大的$j$, 这与AcWing 896. 最长上升子序列 II思路相同. 且最后数值的数目即LIS的长度.

代码实现

第一问 : 最长不上升子序列; 第二问 : LIS.

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010, INF = 1e9;

int n;
int a[N];
int f[N]; //计算最多能拦截多少导弹 : 最长不上升子序列长度
int g[N]; //计算LIS

int main()
{
    while( cin >> a[n] )    n ++ ;

    int res = 0;
    for( int i = 0; i < n; i ++ )
    {
        f[i] = 1;
        for( int j = 0; j < i; j ++ )
            if( a[j] >= a[i] )
            {
                f[i] = max( f[i], f[j] + 1 );
            }
        res = max( res, f[i] );
    }
    cout << res << endl;

    int len = 0;
    g[0] = -INF; //作为哨兵
    for( int i = 0; i < n; i ++ )
    {
        int l = 0, r = len;
        while( l < r )
        {
            int mid = l + r + 1 >> 1;
            if( g[mid] < a[i] ) l = mid;
            else    r = mid - 1;
        }
        len = max( len, r + 1 );
        g[r + 1] = a[i];
    }
    cout << len << endl;

    return 0;
}