算法提高课汇总

算法思路

贪心思想 , 以输入为例 :

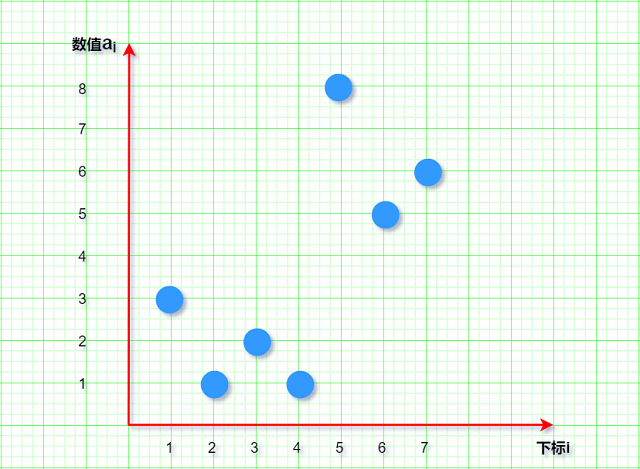
首先观察AcWing 895. 最长上升子序列用DP思路求解时的冗余部分 :

DP求解过程计算以每个元素作为终点时LIS的长度. 以求解$dp[5]$为例, 其重复计算了第1个和第2个元素:
$dp[1] = dp[2] = 1$, 对于第5个元素来说, 如果第1个元素能作为它的上一个元素, 那么第2个元素
也一定能作为它的上一个元素($a_2\lt a_1\lt a_5 $).

贪心思路 : 我们在计算过程中只保留第2个元素, 也即 :
$\;\;\;\;$对所有长度的上升子序列, 只保留其终点数值最小的.

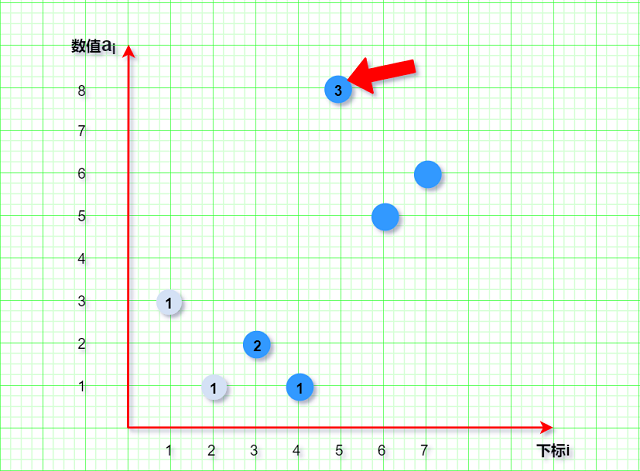
我们标记每个元素作为终点时其LIS的长度, 并用灰色表示其被贪心算法所“抛弃” .

在求第5个元素时 :

在求最后一个元素时 :

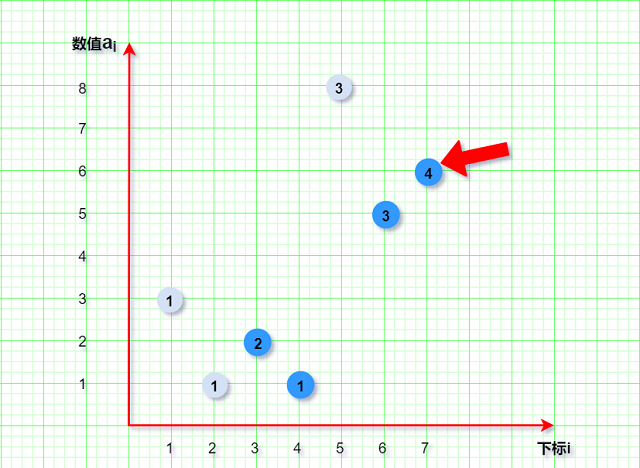
代码实现

用一个f[]数组维护贪心思路的上升序列, 每次遍历元素$a_i$更新这个上升序列 :

• 找到满足$f[j]\lt a[i]$的最大的$j$, 也就是$f[j]\lt a[i]\le f[j+1]$, 用$a[i]$替换$f[j+1]$.

• 如果不存在这样的$f[j+1]$, 则在f[]数组的后面加上元素$a[i]$.

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10, INF = 2e9;

int n;
int a[N], f[N];

int main()
{
    cin >> n;
    for( int i = 1; i <= n; i ++ )  cin >> a[i];

    int len = 0; //len保持f[]的长度
    f[0] = -INF; //作为哨兵, 保证f中一定存在满足小于a[i]的元素
    for( int i = 1; i <= n; i ++ )
    {
        //二分法找到满足f[j] < a[i]的最大元素
        int l = 0, r = len;
        while( l < r )
        {
            int mid = l + r + 1 >> 1;
            if( f[mid] < a[i] ) l = mid;
            else    r = mid - 1;
        }
        f[r + 1] = a[i];
        len = max( len, r + 1 ); //有可能之前不存在f[r+1], f数组长度增加
    }
    cout << len << endl;

    return 0;
}