算法提高课汇总

算法思路

Y氏DP求解 :

状态表示/集合定义 : dp[i]

• 集合 : 以a[i]结尾的所有严格上升子序列

• 属性 : Max(子序列的和最大而不是长度最大)

状态计算/集合划分

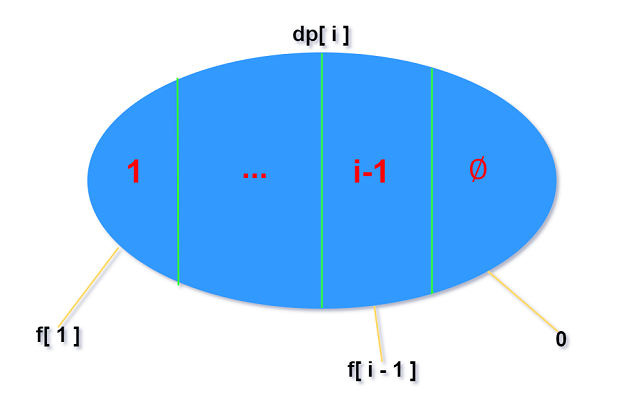
dp[i]代表的集合是严格上升子序列中以a[i]作为结尾的子集. 以a[i]的“上一个”(子序列的倒数第2个)
作为划分依据.

注意 : 可能不存在倒数第2个(集合只有a[i]一个元素). a[j]作为a[i]的“上一个”的条件是
$a[j]\lt a[i]$. 所以为严格起见, 在计算a[i]时, 定义$f[j]$ :
$\;\;\;\;\;\;\;\; f[j] = a[j]\lt a[i]\; ? \;dp[j] : 0$.

和AcWing 895. 最长上升子序列的区别 :权重由1(长度)变为a[i](和)本身.

代码实现

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n;
int a[N], dp[N];

int main()
{
    cin >> n;
    for( int i = 1; i <= n; i ++ )  cin >> a[i];

    int res = 0;
    for( int i = 1; i <= n; i ++ )
    {
        dp[i] = a[i];
        for( int j = 1; j < i; j ++ )
            if( a[j] < a[i] )
            {
                dp[i] = max( dp[i], dp[j] + a[i] );
            }
        res = max( res, dp[i] );
    }
    cout << res << endl;

    return 0;
}