算法提高课汇总

理解题意

题目条件 :

1. 南北两边每个城市都有其对应的另一边的唯一友好城市

2. 每个城市最多与其友好城市建立一座桥

3. 桥与桥之间不能相交

求 : 在满足条件的基础上建立最多的桥.

算法思路

首先理解两座桥相交时满足什么条件. 南边桥的坐标用x[]/北边桥的坐标用y[]表示. x[i]与y[i]互为友好城市.

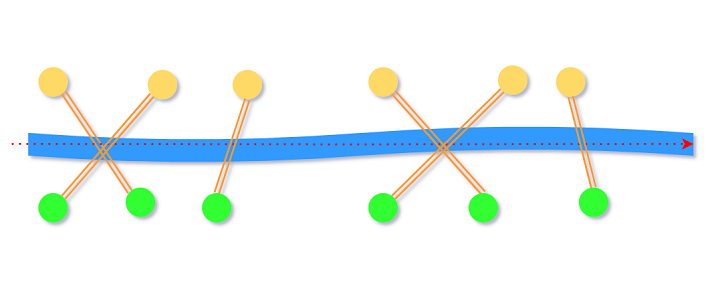
可以观察到, 当$x_i\lt x_j, y_i\gt y_j$时, 第i和第j座桥相交. 我们可以按x[]递增的顺序在满足
不相交条件下选择x[i]: 为了不相交其对应y[i]也要有递增关系. 即我们如果按x[]递增
的顺序选择合法y[], 其选择后的元素也是一个递增序列.

问题转变为从y[]中按x[]递增顺序求解LIS.(合法选择方式与按x[]递增顺序下的y[]的
递增子序列一一对应)

代码实现

#include <iostream>
#include <algorithm>

#define x first
#define y second

using namespace std;

typedef pair<int, int> pii;

const int N = 1e4 + 10;

int n;
pii a[N];
int dp[N];

int main()
{
    cin >> n;
    for( int i = 0; i < n; i ++ )   cin >> a[i].x >> a[i].y;

    sort(a, a + n);

    int res = 0;
    for( int i = 0; i < n; i ++ )
    {
        dp[i] = 1;
        for( int j = 0; j < i; j ++ )
            if( a[j].y < a[i].y )
            {
                dp[i] = max( dp[i], dp[j] + 1 );
            }
        res = max( res, dp[i] );
    }
    cout << res << endl;

    return 0;
}