算法提高课汇总

算法思路

题目要求 :

1. 上山时游览景点按递增顺序

2. 相邻景点编号不同

3. 下山之后就不会再向上

也就是按照先严格上升再严格下降的顺序游览景点 :

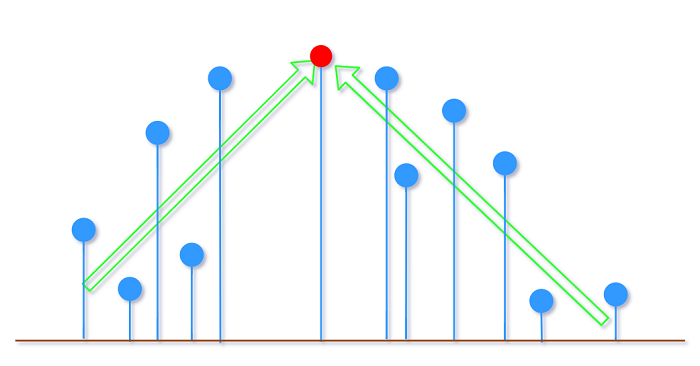
假设我们确定从第i个景点开始下降, 因为左右两边景点游览的选择是相互独立的, 所以实际上我们计算的
是以a[i](景点高度)为终点的LIS和以a[i]为起点的最长下降子序列(从左向右)<-->以a[i]为终点
的LIS(从右向左).

相比于AcWing 1017. 怪盗基德的滑翔翼依次计算两个方向的LIS, 这里是同时计算两个方向的LIS, 求
$max(dp[i] + udp[i]), 1\le i\le N$. 这里$dp[i]和udp[i]$分别表示以a[i]为终点两个方向的LIS的长度.

代码实现

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n;
int a[N];
int dp[N], udp[N];

int main()
{
    cin >> n;
    for( int i = 1; i <= n; i ++ )  cin >> a[i];

    for( int i = 1; i <= n; i ++ )
    {
        dp[i] = 1;
        for( int j = 1; j < i; j ++ )
            if( a[j] < a[i] )
            {
                dp[i] = max( dp[i], dp[j] + 1 );
            }
    }

    for( int i = n; i >= 1; i -- )
    {
        udp[i] = 1;
        for( int j = n; j > i; j -- )
            if( a[j] < a[i] )
            {
                udp[i] = max( udp[i], udp[j] + 1 );
            }
    }

    int res = 0;
    for( int i = 1; i <= n; i ++ )  res = max( res, dp[i] + udp[i] - 1 );

    cout << res << endl;
    return 0;
}