算法提高课汇总

算法思路

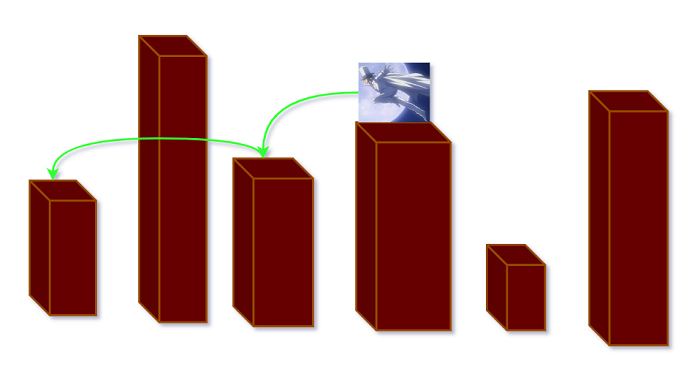
相比于AcWing 895. 最长上升子序列 :

• 怪盗基德的起点任意

• 方向任意, 不过一旦确定方向就不能回头了

假设已经确定起点和方向—第i个楼和向左滑行, 实际上我们求的是 : 以a[i](楼层高度)作为起点的
最长下降子序列(向左)<--->以a[i]为终点的最长上升在子序列(向右).

回忆在LIS问题求解中, 我们从左向右计算每次以i为终点, 也就是计算了所有元素作为终点的情况. 所以
本题和最长上升子序列问题唯一的不同在于需要计算2个方向.

代码实现

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n;
int a[N], dp[N];

int main()
{
    int T;
    cin >> T;
    while( T -- )
    {
        cin >> n;
        for( int i = 1; i <= n; i ++ )  cin >> a[i];

        int res = 0;
        //从左向右计算LIS, 怪盗基德向左滑行
        for( int i = 1; i <= n; i ++ )
        {
            dp[i] = 1;
            for( int j = 1; j < i; j ++ )
                if( a[j] < a[i] )
                {
                    dp[i] = max( dp[i], dp[j] + 1 );
                }
            res = max( res, dp[i] );
        }
        //从右向左计算LIS, 怪盗基德向右滑行
        for( int i = n; i >= 1; i -- )
        {
            dp[i] = 1;
            for( int j = n; j > i; j -- )
                if( a[j] < a[i] )
                {
                    dp[i] = max( dp[i], dp[j] + 1 );
                }
            res = max( res, dp[i] );
        }

        cout << res << endl;
    }
    return 0;
}