算法提高课汇总

算法思路

相比于AcWing 1015. 摘花生问题 :

• 一个人摘花生两次

• 每个格子摘完🥜就没了

状态定义

摘花生问题的状态定义 : dp[i][j] — 从(1,1)到(i,j)的所有合法路径的集合, 用最大花生数代表.
自然的, 本题状态可定义为 :
$\;\;\;\;$dp[i1][j1][i2][j2]—从(1,1)分别走到(i1,j1)和(i2,j2)的所有合法路径的集合, 用最大值表示.

接着我们需要考虑如何处理两条路径经过同一格子时如何处理. 经过同一格子时满足 : $i1 + j1 = i2 + j2$. 由此
我们可以简化问题和状态的定义 : 考虑两个人同步在方格中取数, 也就是其步数/横纵坐标之和相等.

所以可以令$k = i1 + j1 = i2 + j2$, 状态表示为 :

$\;\;\;\;$dp[k][i1][i2]—从(1,1)分别走到(i1,k-j1)和(i2,k-j2)的所有合法路径的集合, 用最大值表示.

问题转化为计算$dp[2n][n][n]$.

状态计算/集合划分

每一条路径均有2个”上1个状态”, 且两条路径相互独立, 所以共有4种划分. 其思考过程与摘花生问题
类似, 且最后状态的表示也是从我们的定义出发.

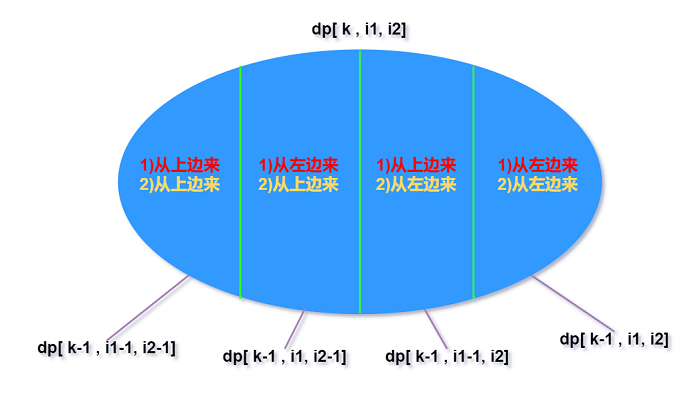
保证每个上1个状态都是取最大值, dp[k][i1][i2]取4个划分的最大.

注意

在每次计算当前状态时都考虑是否两条路径在同一个格子里, 这样就能保证每个状态计算的结果考虑到了
不重复取同一个格子的限制条件.

代码实现

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 15;

int n;
int w[N][N];
int dp[N + N][N][N];

int main()
{
    cin >> n;

    int a, b, c;
    while( cin >> a >> b >> c, a || b || c )    w[a][b] = c;

    for( int k = 2; k <= n + n; k ++ )
    {//循环变量的顺序任意, 只要满足计算当前状态时其计算所依赖状态在之前已经计算完毕即可
        for( int i1 = 1; i1 <= n; i1 ++ )
        {
            for( int i2 = 1; i2 <= n; i2 ++ )
            {
                int j1 = k - i1, j2 = k - i2;
                if( 1 <= j1&&j1 <= n && 1 <= j2&&j2 <= n )
                {
                    int t = w[i1][j1];
                    if( i1 != i2 )  t += w[i2][j2]; //两条路径不在同一个格子里
                    int &x = dp[k][i1][i2];
                    x = max( x, dp[k-1][i1-1][i2-1] );
                    x = max( x, dp[k-1][i1][i2-1] );
                    x = max( x, dp[k-1][i1-1][i2] );
                    x = max( x, dp[k-1][i1][i2] );
                    x += t;
                }
            }
        }
    }

    cout << dp[n + n][n][n] << endl;

    return 0;
}