栈模拟中缀表达式求值过程的简单分析与证明

[TOC]

一. 问题分析

1. 信息提取

+ 和 - 等价, * 和 / 等价

所以只需分析 + 和 *

• * 优先级比 + 大

  $2 + 3 * 2$ 对应的树为

  

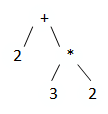
• 同优先级左边大于右边

  $2 + 3 + 2$ 对应的树为

  

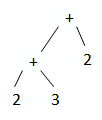
• 括号优先级大于其他

  $(2 + 3) * 2$ 对应的树为

  

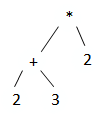
  看起来是 + 的优先级比 * 大, 其实是因为括号的优先级比 * 大

2. 总结特点

• 优先级大的运算符在下面, 优先级小的运算符在上面
• 叶节点都是数字, 内部节点都是运算符, 括号不作为节点, 但会作为一个运算符参与运算符优先级的比较

二. 问题建模

1. 中序遍历表达式树的计算过程

• 任意一个表达式树

  

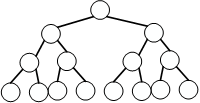
  叶节点是数字, 内部节点是运算符

• 计算过程

  

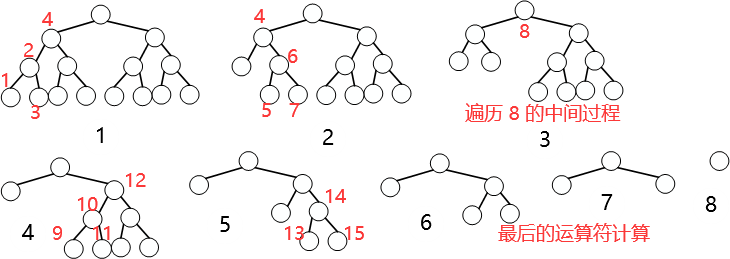
• 遍历节点 1 2 3 后, 则 4 的左子树遍历完, 则计算 4 的左子树的结果, 新节点作为 4 的左孩子节点

• 继续遍历节点 5 6 7, 则 8 的左子树遍历完, 则计算 8 的左子树的结果, 新节点作为 8 的左孩子节点

• 同理, 遍历节点 12 的时候计算其左子树的结果, 新节点作为 12 的左孩子

• 当整棵树遍历完后, 再次逆序计算各运算符的结果, 最后只剩一个节点就是表达式的最终结果

  注意计算 8 的左子树时先计算运算符 6, 然后结果作为运算符 4 的右孩子, 然后计算运算符 4, 其结果作为运算符 8 的左孩子

2. 计算过程分析

如何判断某棵子树被遍历完 ?

• 中序遍历往上走时, 子树遍历完

  例如过程 1 中遍历节点 4 时, 说明 1 2 3 的子树遍历完

• 中序遍历往下走时, 子树未遍历完

  例如过程 2 中遍历节点 6 时, 相对于 4 是往下走的, 此时 8 的左子树未遍历完

如何判断往上走还是往下走 ?

• 注意到运算符优先级大的在下面, 运算符优先级小的在上面
• 所以当目前运算符的优先级比上一运算符优先级小时, 说明是往上走
• 当目前运算符的优先级比上一运算符优先级大是, 说明是往下走

什么时候进行计算 ?

• 往上走时, 因为此时子树遍历完, 需要计算子树的结果, 并将结果作为一个新的节点代替原来的子树

  例如遍历节点 8 时, 计算 8 的左子树, 然后将计算结果作为新的节点代替原来的左子树

三. 问题解法

1. 数据结构

由于是模拟中序遍历树的过程, 所以要用栈数据结构

由于是有运算符和数字两个对象, 所以要用两个栈来存储

2. 算法

遇到各节点后的处理

1. 数字

   数字并不会产生计算过程, 所以只需提取数字, 将数字压栈

2. 括号

   括号分为两个运算符 ( 和 )

   遇到 ( 说明会往下走, 所以只需将 ( 压栈

   遇到 ) 说明会往上走, 所以要计算括号表示的子树的结果, 所以要逆向计算运算符直至遇到 (

3. 普通二元运算符

   如果当前运算符优先级比上一运算符高, 说明是往下走, 则只需将运算符压栈

   如果当前运算符优先级比上一运算符低, 说明是往上走, 则需要一直计算上一运算符直至当前运算符优先级比上一运算符高

3. 核心代码实现

for(int i = 0; i < s.size(); i++)
{
    char c = s[i];              // c 是当前字符
    if(isdigit(c))              // 如果 c 是数字, 就提取数字
    {
        int x = 0, j = i;
        while(j < s.size() && isdigit(s[j])) x = x * 10 + s[j++] - '0';
        i = j - 1;
        num.push(x);
    }
    else if(c == '(') op.push(c);       // 如果 c 是 '(', 就压栈
    else if(c == ')')                   // 如果 c 是 ')', 就一直计算到 '(' 
    {
        while(op.top() != '(') eval();  // eval 函数的功能是计算上一运算符
        op.pop();                       // '(' 出栈
    }
    else                                // 如果 c 是普通运算符, 就一直计算到 c 的优先级比上一运算符高
    {
        while(op.size() && pr[op.top()] >= pr[c]) eval();
        op.push(c);                     // c 入栈
    }
}

四. 算法证明

循环不变式

当前运算符及之前所有运算符的左子树都是形如下图的形状

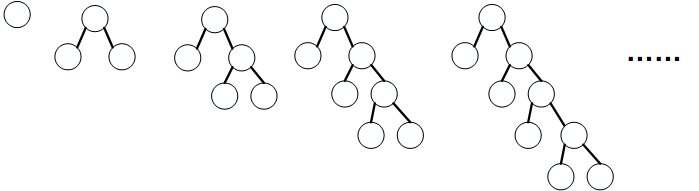
前五个例子, 后面的形状以此类推

证明

初始化

当 i = 0 时, 当前运算符为空, 循环不变式显然成立

保持

假定在某轮循环前, 循环不变式成立

执行该轮 for 循环

c 为当前字符

当 c 为数字时

会提取数字, 然后将数字压栈

则前面的所有子树形状不变, 循环不变式成立

当 c 为 ( 时

会将 ( 压栈

则前面的所有子树形状不变, 循环不变式成立

当 c 为 ) 时

会一直逆序计算运算符直到遇到 (

根据假定, ) 前面的左子树, 即 () 表示的整棵子树是形如下图的形状

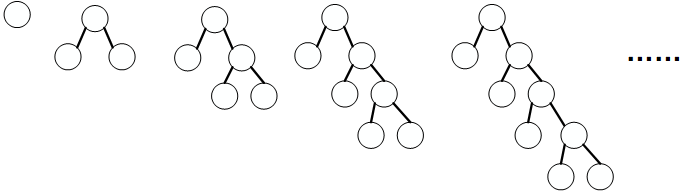
则一直逆序计算运算符直到遇到 ( 会计算 () 表示的整棵子树, 然后将计算结果作为新的节点代替原来的子树

则 () 表示的整棵子树被一个节点代替, 该节点会使得左子树的形状保持循环不变式的形状

例 1 当 () 表示的整棵子树是上图的第一棵子树时

如 2 + (3) , (3) 就是上图的第一棵子树

计算结果是 2 + 3, 对应的子树保持循环不变式的形状

例2 当 () 表示的整棵子树是上图的第一棵子树时

如 2 * (3 + 2), (3 + 2) 就是上图的第二棵子树

计算结果是 2 * 5, 对应的子树保持循环不变式的形状

例3 当 () 表示的整棵子树是上图的第三棵子树时

如 1 + 2 * (3 + 2 * 3) * 3, (3 + 2 * 3) 就是上图的第三棵子树

计算结果是 1 + 2 * 9 * 3, 对应的子树保持循环不变式的形状

注: 此处 “对应的子树” 意为 ‘)’ 运算符前面的运算符的左子树, 即 1 + 2 * 9

当 c 为普通运算符时

会一直逆序计算优先级比自己高的运算符

根据假定, 当前运算符前面的左子树都是形如下图的形状

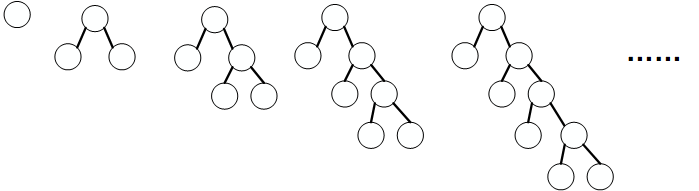
整棵树的形状可以为下图

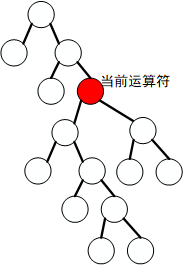
一直逆序计算优先级比自己高的运算符会计算当前运算符的左子树, 并将计算结果作为当前运算符的左孩子

过程如下所示

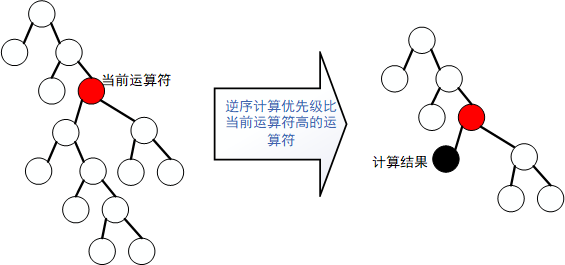
所以当前循环结束后, 循环不变式保持成立

终止

当 for 循环结束后, 整棵树的形状也是循环不变式的形状

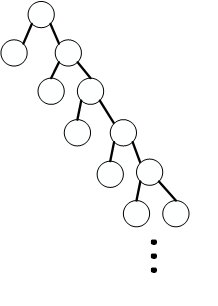
总结

所以在 for 循环结束后, 需要逆序计算运算符直至没有运算符为止, 最终整棵树计算为一个节点, 该节点就是表达式的计算结果

完整代码

#include <iostream>
#include <string>
#include <stack>
#include <unordered_map>

using namespace std;

stack<char> op;
stack<int> num;
unordered_map<char, int> pr = {{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}};

void eval()
{
    int b = num.top(); num.pop();
    int a = num.top(); num.pop();
    char c = op.top(); op.pop();

    int x;
    if(c == '+') x = a + b;
    else if(c == '-') x = a - b;
    else if(c == '*') x = a * b;
    else x = a / b;

    num.push(x);
}

int main()
{
    string s;
    cin >> s;

    for(int i = 0; i < s.size(); i++)
    {
        char c = s[i];
        if(isdigit(c))
        {
            int x = 0, j = i;
            while(j < s.size() && isdigit(s[j])) x = 10 * x + s[j++] - '0';
            i = j - 1;
            num.push(x);
        }
        else if(c == '(') op.push(c);
        else if(c == ')')
        {
            while(op.size() && op.top() != '(') eval();
            op.pop();
        }
        else
        {
            while(op.size() && pr[op.top()] >= pr[c]) eval();
            op.push(c);
        }
    }
    while(op.size()) eval();
    cout << num.top() << endl;

    return 0;
}