算法1
(贪心) $O(n)$
分析
题意:就是要我们找到最小值让机器人可以达到终点
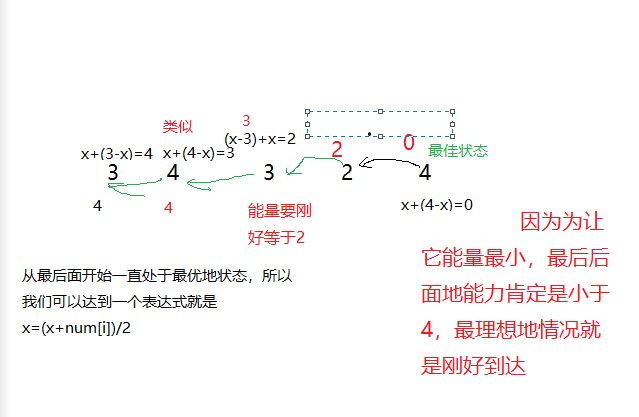
我们先看一组样例:3 4 3 2 4
要想它最小,我们可以直接从最后面开始运算,初始化他的代价为0,我们设初值为x
C++ 代码
#include<bits/stdc++.h>
using namespace std;
const int N=100010;
int num[N];
int n;
int main(){
cin>>n;
for(int i=0;i<n;i++)cin>>num[i];
int res = 0;
for(int i = n - 1; i >= 0; i--){
if((num[i] + res) % 2 == 0)
res = (num[i] + res) / 2;
else
res = (num[i] + res) / 2 + 1;
}
cout<<res<<endl;
}
算法2
(容器vector) $O(n^2)$
#include<bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
vector<int> v(n);
for (int i = 0; i < n; ++i)
cin >> v[i];
int res = 0;
for (int i = n-1; i >= 0; i--) {
if((v[i] + res) % 2 == 0)
res = (v[i] + res) / 2;
else
res = (v[i] + res) / 2 + 1;
}
cout << res << endl;
return 0;
}


参考了大佬的思路,简化了向上取整的步骤,除数是x,只要在被除数上加上x-1,就能达到向上取整的效果。
为什么要除以2啊
所以是为什么除以2
假设当前能量为E(k),下一个点的能量为E(k+1),你可以根据题目给的条件列出E(k+1)与E(k)的关系式的,最后你会得到E(x)=[E(x+1)+H(k+1)]/2,作者的思路是从后往前递推,就是最终最坏的情况是刚好一点能量不剩值为0,然后根据上面的公式一直往前推,得到最起始的值
向上取整是否可以用ceil函数啊
所以二分在哪里?
没二分哈哈哈ovo
题目说有n + 1座建筑,正确的是不是索引应该从0开始到n呢
大佬这个,“的”和“地”没分清啊,看了半天没读懂。
666
这不是都是O(n)算法嘛,算法1算法2有啥区别嘛?
区别就是,换个法存数,就没了
朋友们,我有一点想不通,希望大家可以解释一下:”每次的中间值 上取整,最终的结果依然是正确“是如何保证的?
换句话说,每次中间值上取整会不会导致最终结果偏大?如何证明呢?
这个不会造成结果偏大,具体证明可以代入数据。hhh
我也感觉好神奇,兄弟你想通了没?
数据规模看来没卡掉N方的算法阿
可能是yls 还没有更新测试数据,当时讲课说要加大数据的,hhhhh
万万没想到阿,竟然是个二分,我以为是DP呢
第一种做法不是O(n)的复杂度吗
已修正!
如果是奇数的话整除2会少1的,所以要加上判断条件?
因为C++的int整除是向下取整,所以才要加上那个判断条件吗?