算法分析

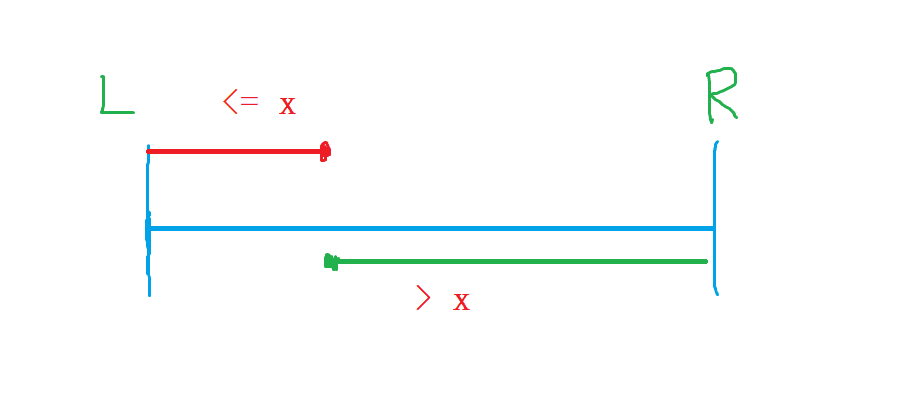
1、找到l = 0，r = Math.min(hMax, wMax)，通过二分找到红色线性质的最右端
2、check()函数表示边长为x大小的饼干是否能分给k个同学

时间复杂度 $O(nlogn)$

参考文献

Java 代码

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;

public class Main {
    static int N = 100010;
    static int[] h = new int[N];
    static int[] w = new int[N];
    static int hMax = Integer.MIN_VALUE;
    static int wMax = Integer.MIN_VALUE;
    static int k;
    static int n;
    //判断边长为x大小的饼干是否能分给k个同学
    public static boolean check(int x)
    {
        int res = 0;
        for(int i = 1;i <= n;i++)
        {
            res += divide(x,i);
        }
        if(res >= k) return true;
        return false;
    }
    //一块饼干能分多少块,x表示边长大小，u表示第几块饼干
    public static int divide(int x,int u)
    {
        int hlen = h[u];
        int wlen = w[u];
        if(x > Math.min(hlen, wlen)) return 0;
        return (hlen/x) * (wlen/x);
    }


    public static void main(String[] args) throws NumberFormatException, IOException {
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        String[] s1 = reader.readLine().split(" ");
        n = Integer.parseInt(s1[0]);
        k = Integer.parseInt(s1[1]);
        for(int i = 1;i <= n;i++)
        {
            String[] s2 = reader.readLine().split(" ");
            h[i] = Integer.parseInt(s2[0]);
            hMax = Math.max(hMax, h[i]);
            w[i] = Integer.parseInt(s2[1]);
            wMax = Math.max(hMax, w[i]);
        }
        int l = 0,r = Math.min(hMax, wMax);
        while(l < r)
        {   //找左端点的最大值
            int mid = (l + r + 1) >> 1;
            if(check(mid)) l = mid;
            else r = mid - 1;
        }
        System.out.println(l);
    }
}

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100000 + 10;
int n, m;
int h[N], w[N];
bool check(int x)
{
    int cnt = 0;
    for(int i = 0;i < n;i ++)
    {
        cnt += (h[i] / x) * (w[i] / x);
    }
    return cnt >= m;
}
int main()
{
    cin >> n >> m;
    for(int i = 0;i < n;i ++)   cin >> h[i] >> w[i];
    int l = 0, r = 100000;
    while(l < r)
    {
        int mid = l + r + 1 >> 1;
        if(check(mid)) l = mid;
        else r = mid - 1;
    }

    cout << l << endl;
    return 0;
}