记录最短路条数
要求最短路计数首先满足条件是不能存在值为0的环,因为存在的话那么被更新的点的条数就为INF了。
要把图抽象成一种最短路树(拓扑图)。
求最短的算法有以下几种(本人学过的)
BFS 只入队一次,出队一次。可以抽象成拓扑图, 因为它可以保证被更新的点的父节点一定已经是最短距离了,并且这个点的条数已经被完全更新过了。这个性质是核心性质。
dijkstra 每个点只出队一次。也可以抽象成拓扑图, 同理由于每一个出队的点一定已经是最短距离,并且它出队的时候是队列中距离最小的点,这就代表他的最短距离条数已经被完全更新了,所以构成拓扑性质。
bellman_ford算法 spfa 本身不具备拓扑序,因为更新它的点不一定是最短距离,所以会出错。举个例子
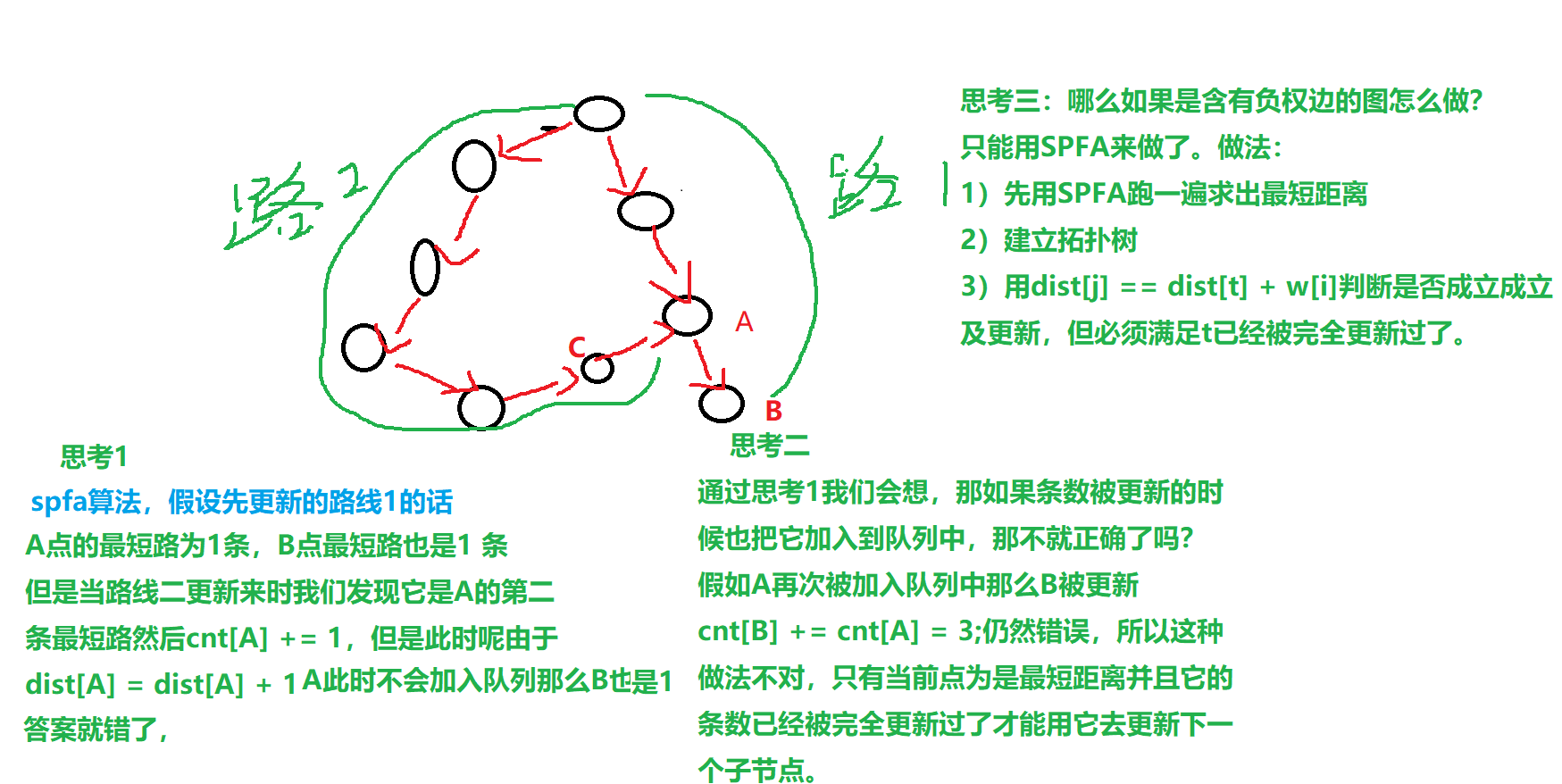
但如果图中存在负权边只能用该算法做,也能做但是比较麻烦
先跑一遍spfa找到每个点的最短距离,把最短路拓扑树建立出来,看哪一条边dist[j] == dist[t] + w[i],然后更新它。


简而言之,dijkstra访问过的边和点拿出来就是拓扑树,因为不会回去更新,BFS同理。
dijkstra和bfs没什么区别
有啊,dij每次只会取队列中离起点最近的点
bfs没有权值,dijkstra有权值,感谢大佬指正
bfs也是最短的点,只不过都为1
dijkstra中每一次出队的点一定是最短距离,感觉最好说成“每一个点出队的第一次都是最短距离”
记录美好生活
%%%%
总结的很清晰哦!
不过那个“思考1”中“dist[A] = dist[A] + 1”是不是写错了?
你为什么能发QQ表情?
应该是写错了