题目要点

这道题目的基本思路就是：枚举所有点的到其余点的距离最大值。但难点在于集合怎么划分，要把一个点的所有可能结果划分为向上（走根节点）走和向下（走子节点）走两类，保证不重不漏。
也就是说我们需要分别结算向上和向下的最大值，取 max 然后再取 min 。
1. 对于向下走，非常简单，直接用 1072 的方法递归遍历子节点即可，不做赘述。
2. 对于向上走，可以把它等效的转换为向下走的问题。

主要说一下怎么转换，直接看下面的图。

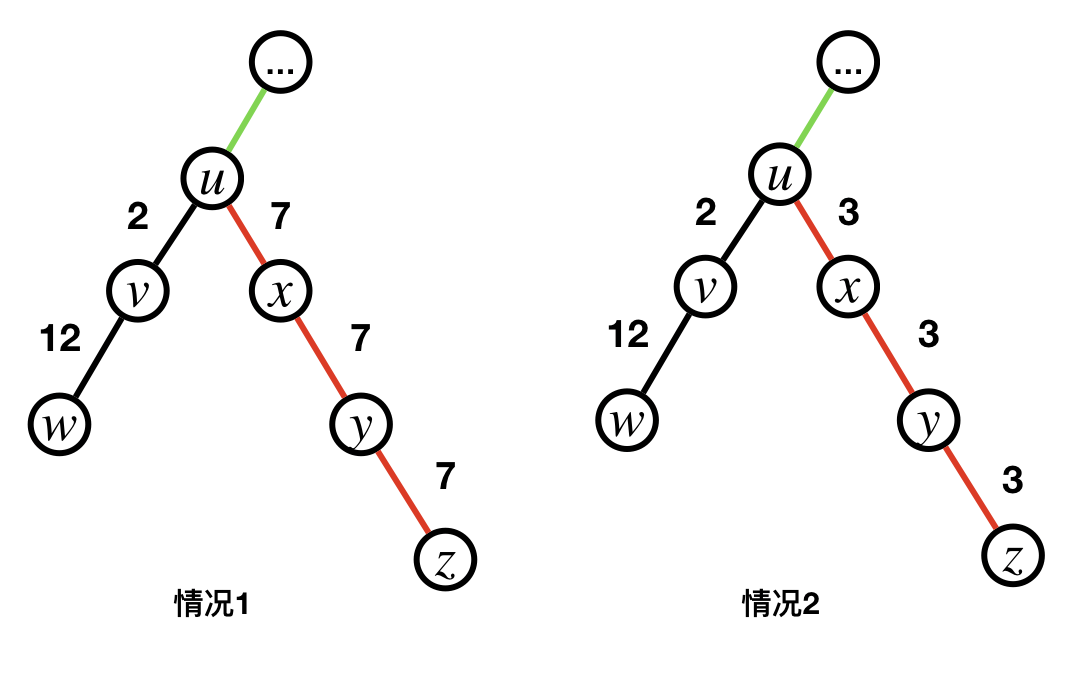
假设我们想求结点$v$的向上的路径最大值，需要比较$v$到$u$后向下（红色）和向上（绿色）这两类路类。对于绿色路径，由于是相同问题，可以直接递归求解；而为了保证红色的最大则要分情况讨论：

1. $v$不是$u$的向下最大路径上的点，经过$u$后直接去找$u$ 向下的 的最大路径（保证是红色中的最大）。
2. $v$是$u$的向下最大路径上的点，如果这时候直接找$u$ 向下的最大（图中为$u,v,w$），就会发现这个路径根本不会向上走，所以需要记录一个次大的路径来保证向上走。

算法1

(DP + DFS)

这里分别用 up 和 down 来表示向上和向下的最大； back 用来表示向下的第二大；由于我们需要知道$v$是否在$u$的最大路径下，所有需要存下每个节点向下最大路径的下一个节点( path)

Python 代码

"""
AcWing 1073. 树的中心
"""


N, INF = 20010, 10000010
e, w, ne, h = [0] * N, [0] * N, [-1] * N, [-1] * N
up, down = [0] * N, [0] * N
back, path = [0] * N, [0] * N

idx = 0


def add_edge(x, y, z):
    global idx
    e[idx] = y
    w[idx] = z
    ne[idx] = h[x]
    h[x] = idx
    idx += 1


def dfs_down(u, root):
    down[u], back[u] = -INF, -INF
    i = h[u]
    while i != -1:
        j = e[i]
        k = w[i]
        i = ne[i]
        if j == root:
            continue
        d = dfs_down(j, u) + k
        if d >= down[u]:
            back[u] = down[u]
            down[u] = d
            path[u] = j
        elif d >= back[u]:
            back[u] = d

    if down[u] == -INF:
        down[u], back[u] = 0, 0
    return down[u]


def dfs_up(u, root):
    i = h[u]
    while i != -1:
        j = e[i]
        k = w[i]
        i = ne[i]
        if j == root:
            continue
        if path[u] == j:
            up[j] = max(up[u], back[u]) + k
        else:
            up[j] = max(up[u], down[u]) + k
        dfs_up(j, u)


def solution():
    n = int(input())
    for i in range(n - 1):
        x, y, z = map(int, input().split())
        add_edge(x, y, z)
        add_edge(y, x, z)

    dfs_down(1, -1)
    dfs_up(1, -1)

    res = INF
    for i in range(1, n + 1):
        res = min(res, max(up[i], down[i]))

    print(res)


if __name__ == '__main__':
    solution()