题目描述

给定一个具有n个顶点的图，要给图上每个顶点染色并且要使相邻的顶点的颜色不同，问是否最多用2种颜色进行染色？没有重边和自环。把相邻顶点染成不同颜色的问题叫做图的着色问题。对图进行染色所需的最小颜色数，称为最小着色数。最小着色数为2的图称为二分图，如下图所示就是一个二分图。下面代码是用来判断是否二分图。

样例

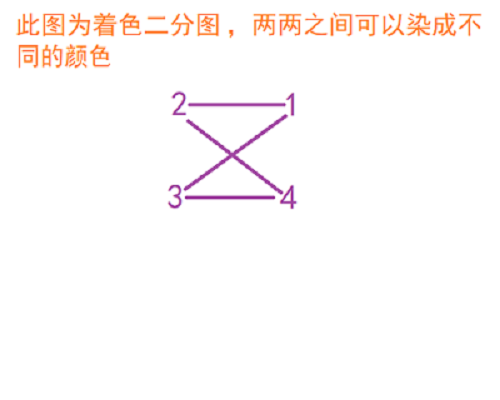
输出

true

算法1

dfs

java 代码

import java.util.Scanner;
import java.util.ArrayList;
import java.util.List;

public class 图的着色_二分图{

    //建邻接表，顶点，邻接点(邻居)
    static class GraphNode{
        int val;
        List<GraphNode> neighbors;
        int color;

        public boolean check=false;

        public GraphNode(int val) {
            this.val=val;
            this.color=color;
        }

        //取邻居
        public GraphNode getNeighbors(int i) {
            return neighbors.get(i);
        }

        //添加邻居
        public void add(GraphNode node) {
            if(this.neighbors==null) {
                this.neighbors=new ArrayList<>();
            }
            this.neighbors.add(node);
        }

        //有几个邻居
        public int size() {
            return this.neighbors.size();
        }
    }

    //c为颜色 1 -1为两种颜色 0为没有颜色
    public static boolean dfs(GraphNode node , int c) {
        node.color=c;
        //遍历所有的邻居
        for(int i=0;i<node.size();i++) {
            GraphNode neighbor=(GraphNode)node.getNeighbors(i);
            //如果邻接点颜色一样，返回false
            if(neighbor.color==c) {
                return false;
            }
            //没有被染色，就染成不同的颜色(-c)进行递归,因为相邻的两个顶点不能染成相同的颜色
            if(neighbor.color==0) {
                boolean flag=dfs(neighbor,-c);
                //我们只看不能染成着色二分图的情况
                if(!flag) {
                    return false;
                }
            }
        }
        //可以染成图的着色二分图
        return true;
    }
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        //添加邻接表，有几个顶点就有几个邻接表，组成图
        GraphNode n1=new GraphNode(1);
        GraphNode n2=new GraphNode(2);
        GraphNode n3=new GraphNode(3);
        GraphNode n4=new GraphNode(4);

         n1.add(n2);
         n1.add(n4);

         n2.add(n1);
         n2.add(n3);

         n3.add(n2);
         n3.add(n4);

         n4.add(n1);
         n4.add(n3);

         System.out.println(dfs(n1,1));  //true 是二分着色图
    }
}