题目描述

我们可以为二叉树 T 定义一个翻转操作，如下所示：选择任意节点，然后交换它的左子树和右子树。

只要经过一定次数的翻转操作后，能使 X 等于 Y，我们就称二叉树 X 翻转等价于二叉树 Y。

编写一个判断两个二叉树是否是翻转等价的函数。这些树由根节点 root1 和 root2 给出。

样例

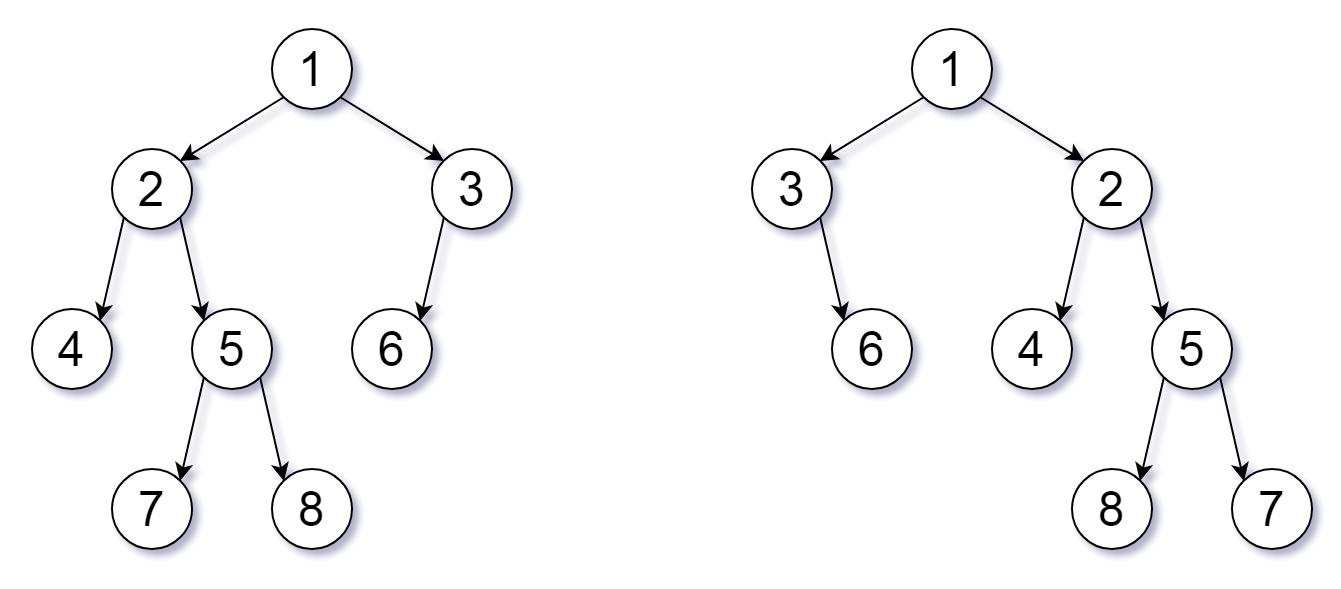
输入：root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]
输出：true
解释：翻转结点 1, 3, 和 5。

注意

• 每棵树最多有 100 个节点。
• 每棵树中的每个值都是唯一的、在 [0, 99] 范围内的整数。

算法

(递归) $O(\min(N1, N2))$

• 每一层都尝试翻转和不翻转两种方式，由于最多只有一种合法，另一种可以在很短时间内排除掉（因为每个结点的值都不同）。

时间复杂度

• 遍历的结点数两棵树中结点较少的树，故时间复杂度为 $O(min(N1, N2))$。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool flipEquiv(TreeNode* root1, TreeNode* root2) {
        if (root1 == NULL && root2 == NULL)
            return true;

        if (root1 == NULL || root2 == NULL)
            return false;

        if (root1 -> val != root2 -> val)
            return false;

        return flipEquiv(root1 -> left, root2 -> left) && flipEquiv(root1 -> right, root2 -> right)
            ||
               flipEquiv(root1 -> right, root2 -> left) && flipEquiv(root1 -> left, root2 -> right);
    }
};