题目描述

给定一个整数数组  nums，求出数组从索引 i 到 j  (i ≤ j) 范围内元素的总和，包含 i,  j 两点。

update(i, val) 函数可以通过将下标为 i 的数值更新为 val，从而对数列进行修改。

样例

示例:

Given nums = [1, 3, 5]

sumRange(0, 2) -> 9
update(1, 2)
sumRange(0, 2) -> 8
说明:

数组仅可以在 update 函数下进行修改。
你可以假设 update 函数与 sumRange 函数的调用次数是均匀分布的。

算法1

区间求和 自然使用 线段树 或者线段数组
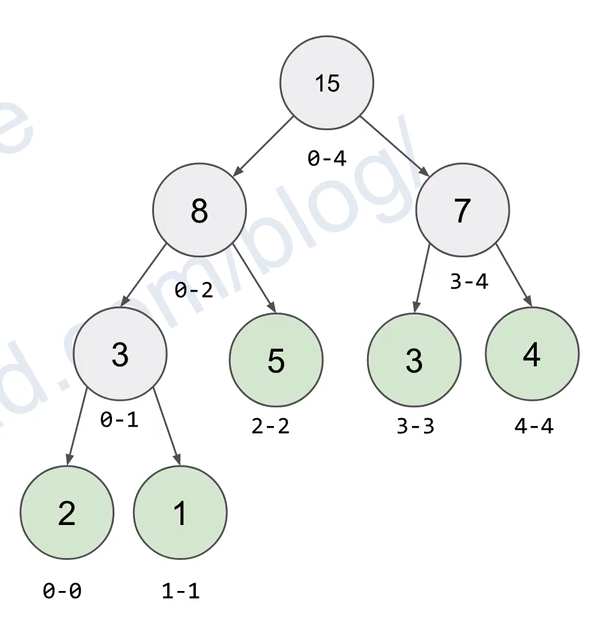
这里以线段树为例
以 空间换时间 记录线段之间的和 最大最小值等
由于是树 即使其中一部分元素改变或者某一个元素改变 更改记录也只是log（n）的复杂度

C++ 代码

class SegmentTreeNode {
public:
    SegmentTreeNode(int start,int end,int sum,
        SegmentTreeNode* left = nullptr,
        SegmentTreeNode* right = nullptr):
        start(start),
        end(end),
        sum(sum),
        left(left),
        right(right){}
    SegmentTreeNode(const SegmentTreeNode&) = delete;
    SegmentTreeNode& operator=(const SegmentTreeNode&) = delete;
    ~SegmentTreeNode() {
        delete left;
        delete right;
        left = right = nullptr;
    }


    int start;
    int  end;
    int sum;
    SegmentTreeNode* left;
    SegmentTreeNode* right;
};

class NumArray {
public:
    NumArray(vector<int> nums) {
        nums_.swap(nums);
        if (!nums_.empty())
            root_.reset(buildTree(0, nums_.size() - 1));
    }

    void update(int i, int val) {
        updateTree(root_.get(), i, val);
    }

    int sumRange(int i, int j) {
        return sumRange(root_.get(), i, j);
    }
private:
    vector<int> nums_;
    std::unique_ptr<SegmentTreeNode> root_;

    SegmentTreeNode* buildTree(int start, int end) {
        if (start == end) {
            return new SegmentTreeNode(start, end, nums_[start]);
        }
        int mid = start + (end - start) / 2;
        auto left = buildTree(start, mid);
        auto right = buildTree(mid + 1, end);
        auto node = new SegmentTreeNode(start, end, left->sum + right->sum,
            left, right);

        return node;
    }

    void updateTree(SegmentTreeNode* root, int i, int val) {
        if (root->start == i && root->end == i) {
            root->sum = val;
            return;
        }
        int mid = root->start + (root->end - root->start) / 2;
        if (i <= mid) {
            updateTree(root->left, i, val);
        }
        else {
            updateTree(root->right, i, val);
        }
        root->sum = root->left->sum + root->right->sum;
    }

    int sumRange(SegmentTreeNode* root, int i, int j) {
        if (i == root->start && j == root->end) {
            return root->sum;
        }
        int mid = root->start + (root->end - root->start) / 2;
        if (j <= mid) {
            return sumRange(root->left, i, j);
        }
        else if (i > mid) {
            return sumRange(root->right, i, j);
        }
        else {
            return sumRange(root->left, i, mid) + sumRange(root->right, mid + 1, j);
        }
    }
};

class NumArray {
public:
    struct Node
    {
        int l, r;
        long long sum, add;
    }tr[100010 * 4];

    void pushup(int u)
    {
        tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
    }
    int emptyFlag =0;
    void pushdown(int u) {
        struct Node& root = tr[u];
        struct Node& left = tr[u << 1];
        struct Node& right = tr[u << 1 | 1];

        if (root.add) {
            left.add += root.add; left.sum += (long long)(left.r - left.l + 1)*root.add;
            right.add += root.add; right.sum += (long long)(right.r - right.l + 1)*root.add;
            root.add = 0;
        }
    }

    void build(int u, int l, int r,const vector<int>& nums)
    {
        if (l == r) { tr[u] = { l,r,nums[r],0 }; }
        else {
            tr[u] = { l,r };
            int mid = l + r >> 1;
            build(u << 1, l, mid, nums);
            build(u << 1 | 1, mid + 1,r, nums);
            pushup(u);
        }
    }

    void modify(int u, int l, int r, int d)
    {
        if (tr[u].l >= l && tr[u].r <= r) {
            tr[u].add += d;
            tr[u].sum += (tr[u].r - tr[u].l + 1)* d;
        }
        else {
            //分段操作
            pushdown(u);
            int mid = tr[u].l + tr[u].r >> 1;
            if (l <= mid) modify(u << 1, l, r, d);
            if (r > mid) modify( (u << 1) + 1, l, r, d);
            pushup(u);
        }
    }


    NumArray(vector<int>& nums) {
        if(nums.empty()) {
            emptyFlag = 1;
            return;
        }
        nums.insert(nums.begin(),0);
        build(1, 1, nums.size()-1, nums);
    }

    void update(int i, int val) {
        if(emptyFlag) return;
        int addV = val - query(1, i + 1, i + 1);
        modify(1, i + 1, i + 1, addV);
    }


    long long query(int u, int l, int r) {
        if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;

        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        long long sum = 0;
        if (l <= mid) sum = query(u << 1, l, r);
        if (r > mid) sum += query(u << 1 | 1, l, r);
        return sum;
    }

    int sumRange(int i, int j) {
        if(emptyFlag) return 0; 
        return (int)query(1,i+1,j+1);
    }
};