题目描述

(此题是 交互式问题)

在用笛卡尔坐标系表示的二维海平面上，有一些船。每一艘船都在一个整数点上，且每一个整数点最多只有 1 艘船。

有一个函数 Sea.hasShips(topRight, bottomLeft)，输入参数为右上角和左下角两个点的坐标，当且仅当这两个点所表示的矩形区域（包含边界）内至少有一艘船时，这个函数才返回 true，否则返回 false。

给你矩形的右上角 topRight 和左下角 bottomLeft 的坐标，请你返回此矩形内船只的数目。题目保证矩形内 至多只有 10 艘船。

调用函数 hasShips 超过 400 次 的提交将被判为 错误答案（Wrong Answer）。同时，任何尝试绕过评测系统的行为都将被取消比赛资格。

样例

输入：
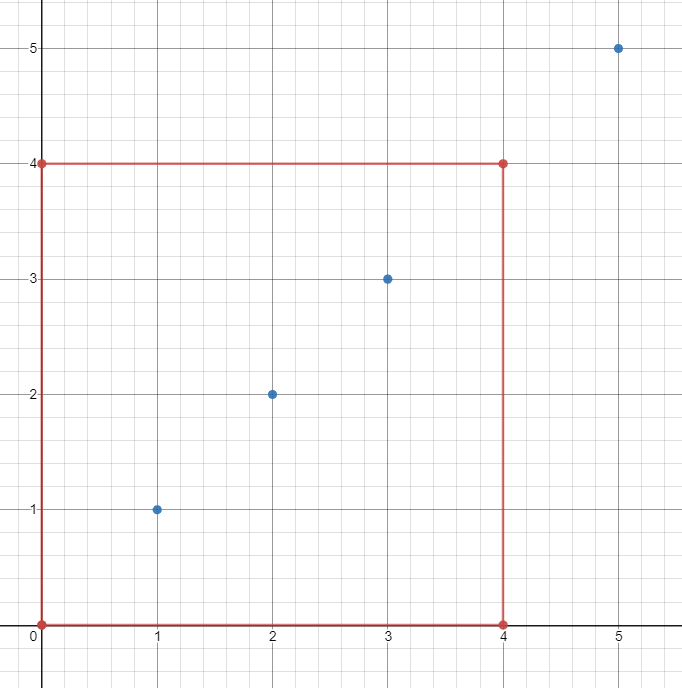
ships = [[1,1],[2,2],[3,3],[5,5]], topRight = [4,4], bottomLeft = [0,0]
输出：3
解释：在 [0,0] 到 [4,4] 的范围内总共有 3 艘船。

限制

• ships 数组只用于评测系统内部初始化。你无法得知 ships 的信息，所以只能通过调用 hasShips 接口来求解。
• 0 <= bottomLeft[0] <= topRight[0] <= 1000
• 0 <= bottomLeft[1] <= topRight[1] <= 1000

算法

(分治)

1. 我们每次将一个矩形平均分为四部分，对每一部分内部是否有船进行一次判断，如果有，则递归进入。
2. 递归函数返回当前矩形内船的总和。

C++ 代码

/**
 * // This is Sea's API interface.
 * // You should not implement it, or speculate about its implementation
 * class Sea {
 *   public:
 *     bool hasShips(vector<int> topRight, vector<int> bottomLeft);
 * };
 */

class Solution {
public:
    int countShips(Sea sea, vector<int> topRight, vector<int> bottomLeft) {
        if (bottomLeft == topRight)
            return sea.hasShips(topRight, bottomLeft);

        int x = (bottomLeft[0] + topRight[0]) >> 1;
        int y = (bottomLeft[1] + topRight[1]) >> 1;

        int tot = 0;
        if (sea.hasShips({x, y}, bottomLeft)) {
            tot += countShips(sea, {x, y}, bottomLeft);
        }

        if (x + 1 <= topRight[0]
            && sea.hasShips({topRight[0], y}, {x + 1, bottomLeft[1]})) {
            tot += countShips(sea, {topRight[0], y}, {x + 1, bottomLeft[1]});
        }

        if (y + 1 <= topRight[1]
            && sea.hasShips({x, topRight[1]}, {bottomLeft[0], y + 1})) {
            tot += countShips(sea, {x, topRight[1]}, {bottomLeft[0], y + 1});
        }

        if (x + 1 <= topRight[0] && y + 1 <= topRight[1]
            && sea.hasShips(topRight, {x + 1, y + 1})) {
            tot += countShips(sea, topRight, {x + 1, y + 1});
        }

        return tot;
    }
};