最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

给定一棵包含 $n$ 个结点的 树，以及 树 上的 $n-1$ 条边

我们需要在这 $n$ 个结点中，选择一定数量的结点放上 哨兵

最终要求，树中任意 $n-1$ 条边的左右两端，至少有一个结点上放置了 哨兵

求解一个 方案，该方案满足上述要求，且放置的哨兵数量 最少，输出该 方案 放置的 哨兵数量

分析

这是基础课原题 AcWing 285. 没有上司的舞会

显然我们不能 暴力枚举 树中所有结点 选(1) 与 不选(0) 的状态（时间复杂度 为 $O(2^n)$）

因此，会想到采用 分治 思想：
考虑以结点 $u$ 为 根节点 的子树，该子树所有的 方案，可以由当前结点 放 或 不放哨兵 进行划分

这也是一种 状态机模型，我简略的绘制一下这个状态机：

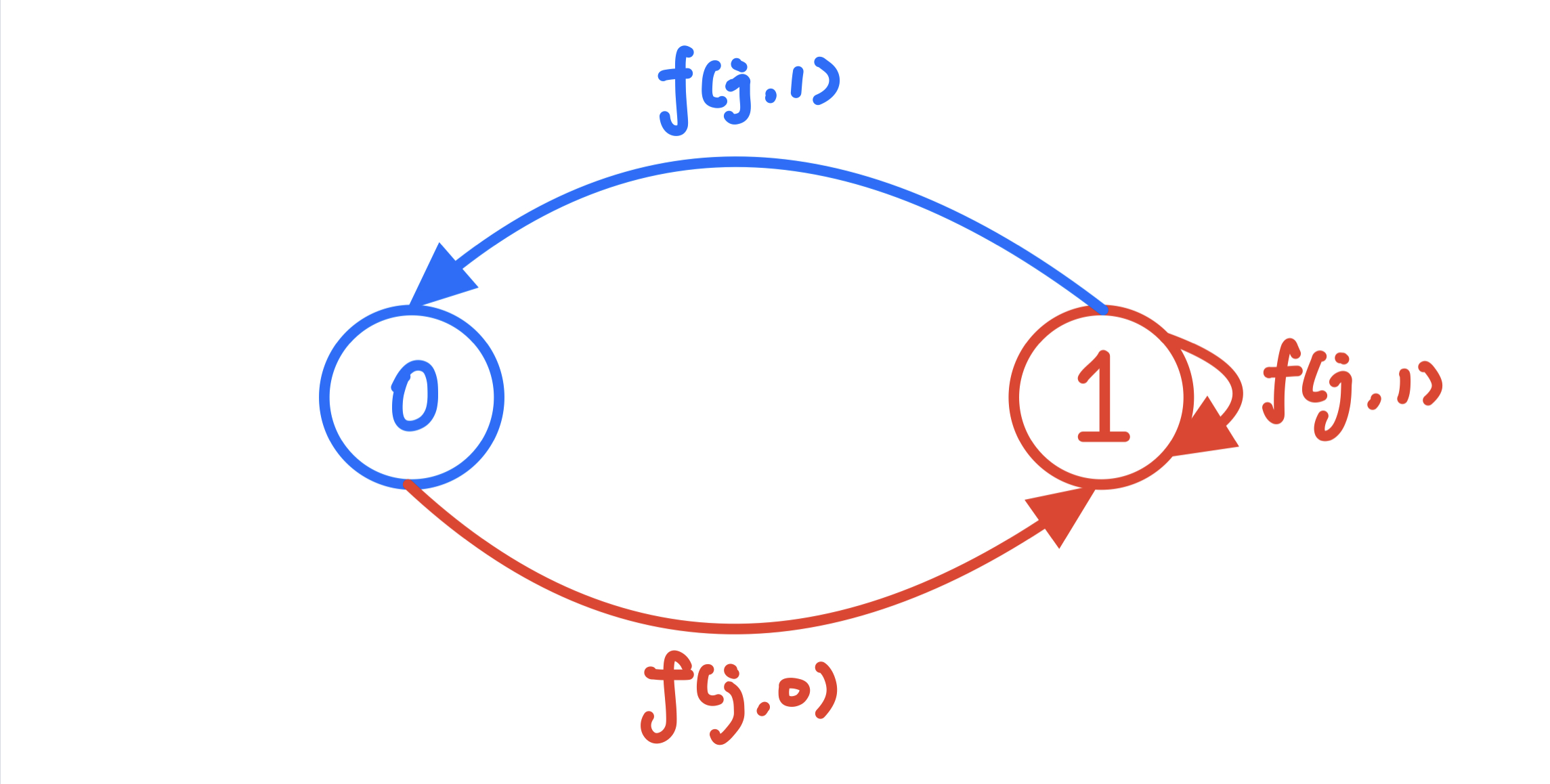
• 如果当前结点放置了哨兵(1)，则该子树中，连向他的边的另一端，可以放置(1)，也可以不放置(0)
• 如果当前结点没有放哨兵(0)，则该子树中，连向他的边的另一端，必须可以放置(1)

这样就可以轻易想到 状态的定义 了，具体如下：

闫氏DP分析法

状态表示 — $f_{i,1/0}$ 集合： 以结点 $i$ 为 根节点 的子树，在 $i$ 上放置哨兵$(1)$ 和不放哨兵$(0)$ 的方案

状态表示 — $f_{i,1/0}$ 属性： 方案中，放置的哨兵数量 最少

状态计算：

在 $i$ 上放置哨兵$(1)$：

$$f_{i,1} = \sum_{i_{ch}} \min(f_{i_{ch}~,0}, f_{i_{ch}~,1}) \quad(i_{ch} \in \{ver | ver\text{是 i 的子节点}\})$$

在 $i$ 上不放哨兵$(0)$：

$$f_{i,0} = \sum_{i_{ch}} f_{i_{ch}~,1} \quad(i_{ch} \in \{ver | ver\text{是 i 的子节点}\})$$

Code

时间复杂度： $O(n)$

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1510;

int n;
int h[N], e[N], ne[N], idx;
int f[N][2];
bool not_root[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u)
{
    f[u][0] = 0, f[u][1] = 1;  //initialize
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        dfs(j);
        f[u][0] += f[j][1];
        f[u][1] += min(f[j][0], f[j][1]);
    }
}
int main()
{
    while (~scanf("%d", &n))
    {
        memset(h, -1, sizeof h); idx = 0;
        memset(not_root, 0, sizeof not_root);
        for (int i = 0; i < n; i ++ )
        {
            int a, b, siz;
            scanf("%d:(%d) ", &a, &siz);
            while (siz -- )
            {
                scanf("%d", &b);
                add(a, b);
                not_root[b] = true;
            }
        }
        int root = 0;
        while (not_root[root]) root ++ ;
        dfs(root);
        printf("%d\n", min(f[root][0], f[root][1]));
    }
    return 0;
}