历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 1075. 数字转换【树形DP】原题链接中等

作者：

一只野生彩色铅笔 , 2021-09-01 22:23:06 , 所有人可见 , 阅读 5169

79

7

最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

如果一个数 $x$ 的 约数之和 $y$ （不包括他本身）比他本身小，那么 $x$ 和 $y$ 可以 互相转换

给定一个正整数 $n$ ，求出正整数 $[1,n]$ 构成的字符集：在不出现重复数字的情况下，能进行的最大变换步数

分析

本题不重在代码思路，重在模型建图，因此我们来一步步分析

根据题意，单看一个数字 $x$ ，那么他能转换到的数有：

$x$ 的约数之和 $x’$ （ $x’ < x$ ）
所有大于 $x$ ，且约数之和等于 $x$ 的数 $x_i$

那么我们就能绘出如下抽象图示了：

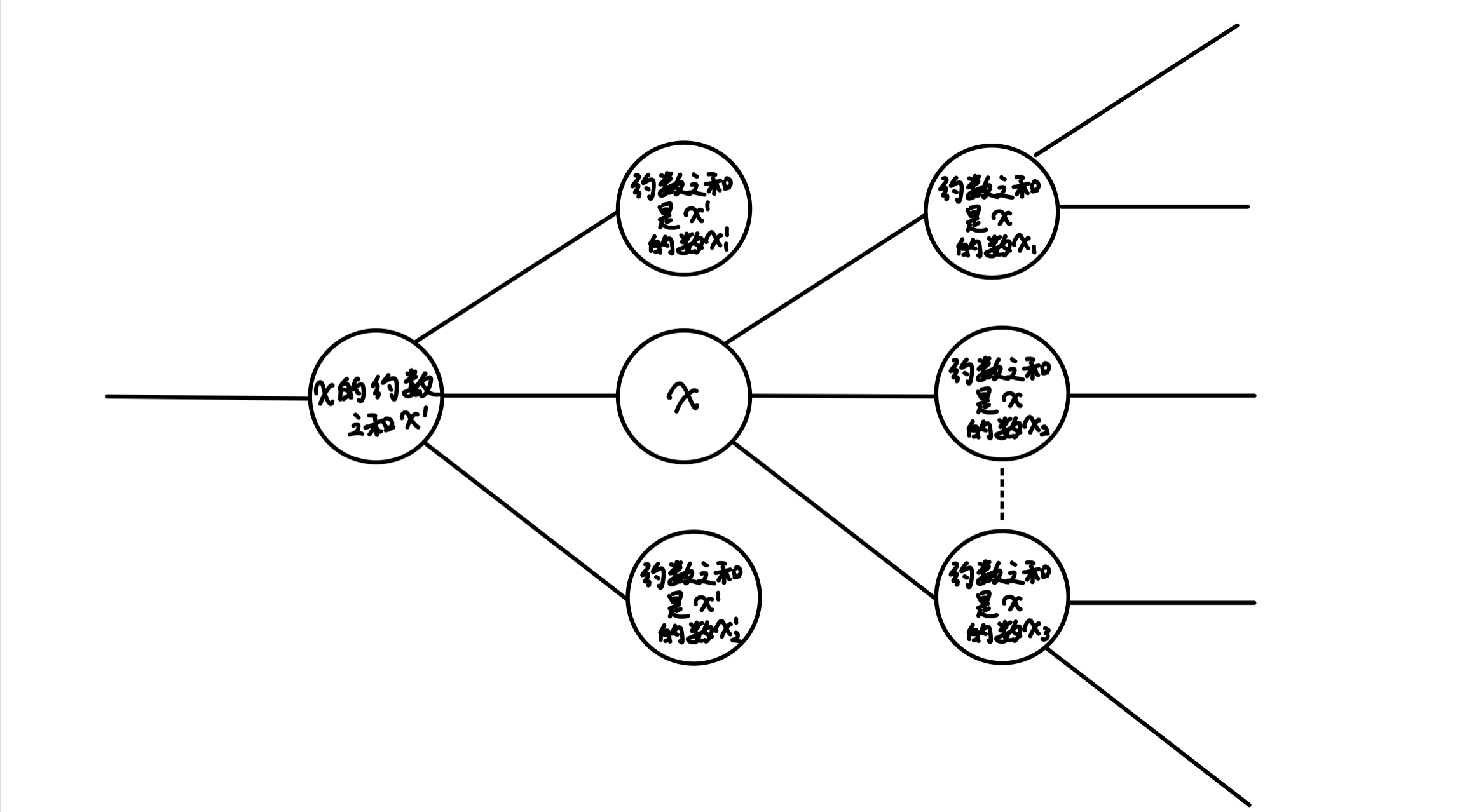
由于任意正整数 $x$ ，的 约数之和 是 唯一的，且本题要求只有约数之和小于自身才能转换

故对于所有的 $x$ 来说，他向小于自己的数转换的边至多只有一条，那就是 $x$ 的 约数之和 $x’(x’<x)$

这样一个图论模型我们就很熟悉了，我们把每一个数看作一个点，把上述这个转换看作该点的入边

每一个点，至多只有一条 入边，这就是森林呀

建好图后，本题就 等价于 找出一个森林中，直径最长 的树，并求出该树的直径

那就要用到我们的 树形DP 了，指路 AcWing 1072. 树的最长路径【树形DP】

Code

时间复杂度： $O(n\log\log n)$

#include <iostream>
#include <cstring>

using namespace std;

const int N = 5e4 + 10;

int n, fsum[N];
int h[N], e[N], ne[N], idx;
int d1[N], d2[N], res;

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u)
{
    if (d1[u]) return;  //记忆化搜索
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        dfs(j);
        if (d1[j] + 1 >= d1[u]) d2[u] = d1[u], d1[u] = d1[j] + 1;
        else if (d1[j] + 1 > d2[u]) d2[u] = d1[j] + 1;
    }
    res = max(res, d1[u] + d2[u]);
}
int main()
{
    memset(h, -1, sizeof h);
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ )
        for (int j = 2; j <= n / i; j ++ )
            fsum[i * j] += i;
    for (int i = 2; i <= n; i ++ )
        if (fsum[i] < i)
            add(fsum[i], i);
    for (int i = 1; i <= n; i ++ ) dfs(i);
    printf("%d\n", res);
    return 0;
}

34 评论

一只野生彩色铅笔 2022-03-10 15:09

本篇下不再讨论是否答案一定是以 1 为根的子树了

之前有好几位同学来理论，都没给出证明，然后自己删评了

整数域内存在好几个独立的环，大家都是会编程的，可以自己去搜一下 1 ～ 100000 以内的数

怎么证明答案一定在 1 的子树里，只能给出直观直觉，我是不会数学证明的，如果你认为是的话，请在下方给出严谨数学证明

wyjjjjj 2022-06-28 15:09

原本是要建双向边的，但是因为我每次dfs都是从根节点开始的，所以可以建有向边，因为有根树的直径一定会经过根节点。原本求树的直径要建无向边是因为不确定该点一定是根节点

Eurus_ 2022-08-01 21:56

看了你的这条评论，我才懂了为啥只建单向边，谢谢

笨蛋1 2022-08-08 09:12

有根树的直径一定会经过根节点，这句话不对吧？只能说直径一定会经过从根节点递归到的某个节点

比博燃 2022-11-06 22:38 回复了笨蛋1 的评论

学长说的很对

热衷算法每一天 6天前 ·江苏回复了笨蛋1 的评论

赞同

最傻的猪 2022-04-30 21:24

有没有这样的情况，一个数同时是两个大于它的数的约数之和啊？

最傻的猪 2022-04-30 21:36

有的🐙，刚刚自己写了个程序看了下

糖豆 2022-02-14 13:41

请问大神，为什么一定要加记忆化呢？我尝试去掉记忆化，感觉最多就是TLE，结果答案错了，不明白道理

Makisekurisu_4 2022-02-14 16:10

被重复计算了. 可以看看上面那个图

fulvia 2024-03-01 18:52

你想明白了吗，我也遇到这个问题了

fulvia 2024-03-01 18:53 回复了 Makisekurisu_4 的评论

为什么呢，具体是什么情况出的问题？

fulvia 2024-03-04 13:56

好像重复更新会把d2更新了，d2会比原来大

fulvia 2024-03-04 13:57 回复了 fulvia 的评论

出错的数据d1和d2都相等

Moon_light 2023-09-24 15:01

dfs(1) 答案也能AC，有什么区别吗

baobaojiao 2022-11-03 17:22

约数之和是1的一定是个素数，所有数的约数里都有1，可并不是所有数的约数都只有1

布克波波 2022-11-25 14:16

Robate 2023-05-13 14:27

最傻的猪 2022-04-30 21:45

#include <iostream>
#include <cstring>

using namespace std;

const int N = 5e4 + 10;

int n, fsum[N];
int h[N], e[N], ne[N], idx;
int d1[N], d2[N], res;

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u)
{
    //if (d1[u]) return;  //记忆化搜索
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        dfs(j);
        if (d1[j] + 1 >= d1[u]) d2[u] = d1[u], d1[u] = d1[j] + 1;
        else if (d1[j] + 1 > d2[u]) d2[u] = d1[j] + 1;
    }
    res = max(res, d1[u] + d2[u]);
}
int main()
{
    memset(h, -1, sizeof h);
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ )
        for (int j = 2; j <= n / i; j ++ )
            fsum[i * j] += i;
    for (int i = 2; i <= n; i ++ )
        if (fsum[i] < i)
            add(fsum[i], i);
    dfs(1);
    printf("%d\n", res);
    return 0;
}

答案如果在根为1的树里的话，好像就不用记忆化那一步了

derderderde 2022-03-10 14:27

其实求解目标是：max(d1[1], d2[1])

typedef 2021-11-02 10:58

我感觉这个add应该加两条边吧（

一只野生彩色铅笔 2021-11-05 23:16

小的数字往大的数字上连一条就够了

搜了根，这个树的直径就找出来了，没有反向搜的必要

typedef 2021-11-06 08:09 回复了一只野生彩色铅笔的评论

确实是

typedef 2021-11-06 08:10 回复了一只野生彩色铅笔的评论

太卷了，半夜12点回复消息

此账号已注消 2022-01-29 20:35 回复了 typedef 的评论

Orz ，这也太卷了，维持一定的顺序就可以不用建双向边Orz

椒盐土豆 2022-03-17 00:53 回复了 typedef 的评论

半夜十二点发现回消息不是更卷吗

max.D.well 2022-04-01 01:08 回复了一只野生彩色铅笔的评论

为什么从小得数字往大的数字上连边就可以了，而从大的数字连边往小得数字连边就不行

最傻的猪 2022-04-30 21:41 回复了 max.D.well 的评论

一个数可能是多个树的约数之和

uhgariej 2021-09-24 11:17

“建好图后，本题就等价于找出一个森林中，直径最长的树，并求出该树的直径”, 其实我们找以1为根的树, 单单求这颗树的直径就是答案.

一只野生彩色铅笔 2021-09-24 11:29

直观上看应该是对的，以1为根的树就是1到n的所有素数个数加上约数和为素数的子树的节点个数

但是严格数学证明好像有点复杂

大佬有什么好的证明方法，可以写出来让我观摩观摩吗 QAQ

max.D.well 2022-04-01 01:47 回复了一只野生彩色铅笔的评论

因为这颗树有一个性质就是不存在任何约束和大于等于节点值得节点。及证明一个数x，其约数和（不包含x本身）小于x时，其所有约数都满足这个性质（约数和小于本身）。证明：假设如果数x，满足约束和小于x，且存在约数y满足约数和大于等于y，设 z = x / y, y1 .. yn 是x的约数，则z1 = z * y1, zn = z * yn也都是x的约数, z1 + … zn = z * (y1 + y2 .. yn） >= z * y = x; 与假设相反。