AcWing. 896 最长上升子序列 II

题目描述

给定一个长度为N的数列，求数值严格单调递增的子序列的长度最长是多少。

样例

输入：
7
3 1 2 1 8 5 6
输出：
4
解释：找到最长的上升子序列1 2 5 6， 长度为4

限制

• $1 ≤ N ≤ 100000$
• $−10^9 ≤ 数列中的数 ≤ 10^9$

算法1（TLE）

(贪心 + 暴力枚举) $O(n^2)$

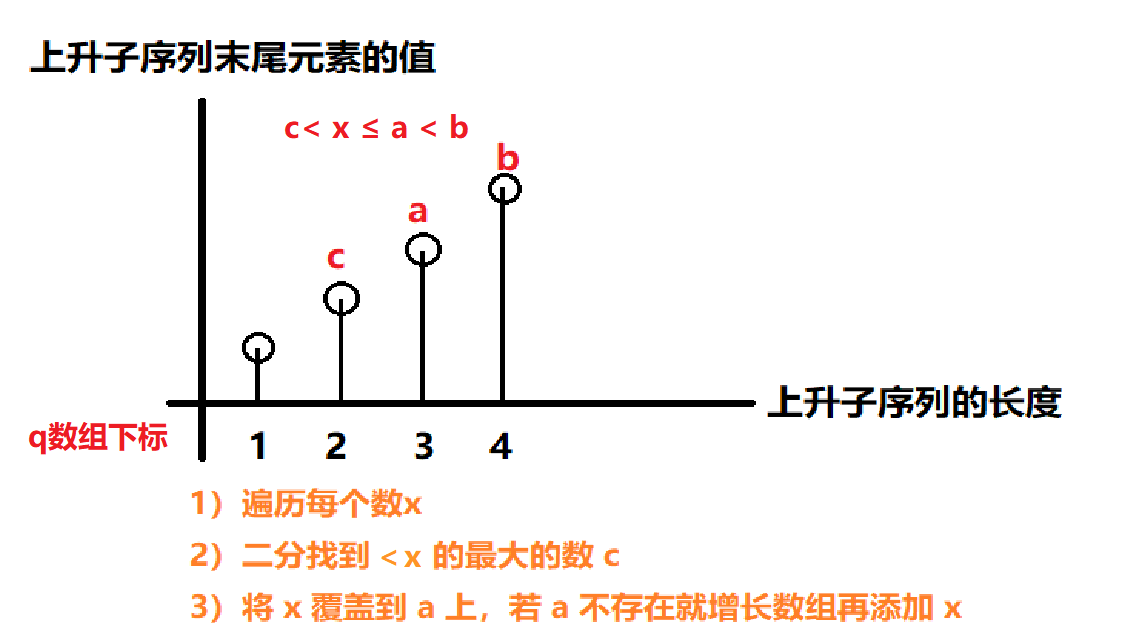
• 贪心思路：较小的数开头的数作为的子序列 比 较大的数作为开头的子序列 更好
• 贪心步骤：
  • 开一个数组q[i]，存的是以长度为i的上升子序列中末尾元素最小的数，
  • q[]一开始是空集，长度为0
  • 遍历每个数x，对于当前数x, 先找到一个最大的小于x的数c感谢@sort：
    • 情况1：若找不到c, 扩大q[]的长度并记录当前数x
    • 情况2：若找到c, 就存在一个不等式c < x ≤ a < b, 则将x覆盖a的位置

时间复杂度

• 遍历每个数是 $O(n)$
• 遍历 q 数组每个数, 找到一个最大的小于当前数x的数c，最坏情况需要枚举所有数 $O(n)$
• 因此时间复杂度是 $O(n^2)$
• 由于本题的N = 100000, (10^5)^2 = 10^10 会 TLE

C++ 代码

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1e5 + 10;
int n;
int a[N], q[N];

int main(){
    cin >> n;
    for(int i = 0; i < n; i ++) scanf("%d", &a[i]);

    int len = 0;
    for(int i = 0; i < n; i ++){
        int k = 0;
        while(k < len && q[k] < a[i]) k ++;
        q[k] = a[i];
        if (k >= len) len ++;
    }

    cout << len << endl;
    return 0;
}

算法2

(贪心 + 二分) $O(nlog{n})$

• 基于算法1的单调性：找到一个最大的小于等于当前数的数, 我们可以用 二分 来优化
• 二分的思路：
  • 先定义边界，l = 0, r = len, 其中len是q数组的长度
  • 然后确定check函数, 可以先找到不等式中c < x ≤ a ≤ b的c
    • 通过q[r + 1] = a[i]来将x覆盖a的值
    • 同时也要考虑算法1的情况1, 需要扩大q数组的长度
      • 即r + 1 > len时, 表示超出了二分边界，这时就要len ++更新q的长度

时间复杂度

• 遍历每个数是 $O(n)$
• 遍历q数组每个数, 找到一个最大的小于当前数x的数c $O(log{n})$
• 因此时间复杂度是 $O(nlog{n})$

C++ 代码

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1e5 + 10;
int n;
int a[N], q[N];

int main(){
    cin >> n;
    for(int i = 0; i < n; i ++) cin >> a[i];

    int len = 0;
    for(int i = 0; i < n; i ++){
        int l = 0, r = len; // 二分找到最大的小于当前数x的数c
        while(l < r){
            int mid = l + r + 1 >> 1;
            if(q[mid] < a[i]) l = mid;
            else r = mid - 1;
        }

        q[r + 1] = a[i];
        if(r + 1 > len) len ++;
    }

    cout << len << endl;
    return 0;
}